搜索
【题目】已知⊙O1与⊙O2的圆心距O1O2＝6cm，且两圆的半径满足一元二次方程x2-6x+8=0，则两圆的位置关系为 ( )
A. 外切 B. 内切 C. 外离 D. 相交
参考答案：
【答案】A
【解析】试题解析：解方程x2-6x+8=0得：
x1=2，x2=4，
∵O1O2=6，x2-x1=2，x2+x1=6，
∴O1O2=x2+x1．
∴⊙O1与⊙O2相外切．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=ax+b与反比例函数y=
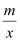（x＞0）的图象交于A（1，4），B（4，n）两点，与x轴，y轴分别交干C，D两点．
（1）m= ，n= ；若M（xl，y1），N（x2，y2）是反比例函数图象上两点，且0＜xl＜x2，则yl y2（填“＜”或“＝”或“＞”）；
（2）若线段CD上的点P到x轴，y轴的距离相等．求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若直线y=kx+b与直线y=2x平行，且与y轴相交于点（0，–3），则直线的函数表达式是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】其中考试后，班里有两位同学各科平均成绩相同，但是标准差不同，以下说法正确的是（ ）
A. 平均分数相等说明两名同学各科学习成绩一样
B. 标准差较大的说明各科成绩比较稳定
C. 标准差较大的说明成绩比较好
D. 标准差小的比标准差大的各科成绩之间差异较小
-
科目： 来源： 题型：
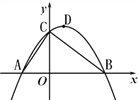
查看答案和解析>>【题目】如图,已知点A的坐标为（-2，0），直线
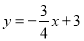与x轴、y轴分别交于点B和点C，连接AC，顶点为D的抛物线
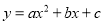过A、B、C三点.（1）求抛物线的解析式及顶点D的坐标；
（2）设抛物线的对称轴DE交线段BC于点E，P是第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标.
（3）设点M是线段BC上的一动点，过点M作MN∥AB，交AC于点N，点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒），当t（秒）为何值时，存在△QMN为等腰直角三角形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE与射线AF交于点G.
（1）若OE平分∠BOA，AF平分∠BAD，∠OBA=42°，则∠OGA= ；
（2）若∠GOA=
∠BOA，∠GAD=∠BAD，∠OBA=42°，则∠OGA= ；（3）将（2）中的“∠OBA=42°”改为“∠OBA=
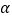”，其它条件不变，求∠OGA的度数.（用含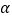的代数式表示）（4）若OE将∠BOA分成1︰2两部分，AF平分∠BAD，∠ABO=
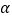（30°<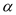
<90°） ，求∠OGA的度数.（用含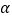的代数式表示）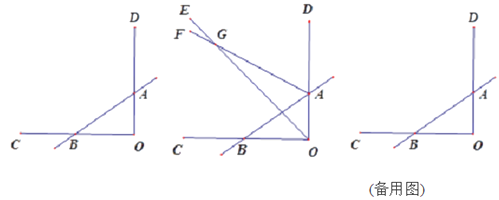
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
（1）△ABC的面积为______；
（2）将△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B′，补全△A′B′C′；
（3）若连接AA′，BB′，则这两条线段之间的关系是______；
（4）在图中画出△ABC的高CD．
相关试题
