【题目】已知,△ADB内接于⊙O,DG⊥AB于点G,交⊙O于点C,点E是⊙O上一点,连接AE分别交CD、BD于点H、F.
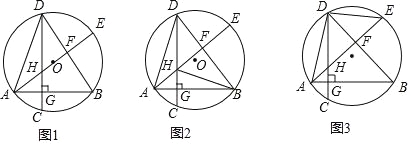
(1)如图1,当AE经过圆心O时,求证:∠AHG=∠ADB;
(2)如图2,当AE不经过点O时,连接BC、BH,若∠GBC=∠HBG时,求证:HF=EF;
(3)如图3,在(2)的条件下,连接DE,若AB=8,DH=6,求sin∠DAE的值.
参考答案:
【答案】见解析.
【解析】
试题分析:(1)如图1中,连接BE,由DG∥BE,推出∠AEB=∠AHG,由∠ADB=∠AEB,即可推出∠ADB=∠AHG.
(2)连接AC、DE,EB、AC、BC.只要证明HG=CG,∠EDB=∠CDB,根据等腰三角形三线合一即可证明.
(3)过点O作ON⊥DE,OM⊥AB垂足分别为N、M,连接OD、OE、OA、OB.只要证明△NOE≌△MBO,推出NE=OM=3,OB=![]() =5,在RT△OMB中,根据sin∠OBM=
=5,在RT△OMB中,根据sin∠OBM=![]() ,计算即可.
,计算即可.
试题解析:证明:(1)如图1中,连接BE,
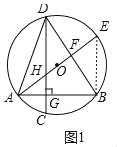
∵AE是⊙O的直径∴∠ABE=90°,
∵DG⊥AB,
∴∠ABE=∠AGD=90°,
∴DG∥BE,
∴∠AEB=∠AHG,
∵∠ADB=∠AEB
∴∠ADB=∠AHG.
(2)连接AC、DE,EB、AC、BC.
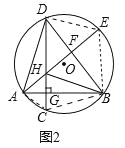
∠GBC=∠HBG,DG⊥AB
∴∠GHB=∠BCH,BH=BC,
∴HG=CG,
∴AH=AC,∠AHC=∠HCA,∠BAC=∠HAG
∵∠AED=∠ACH,∠DHE=∠AHC,
∴∠AED=∠DHE,
∴DH=DE,
∵∠EDB=∠EAB,∠CDB=∠BAC,
∴∠EDB=∠CDB,
∴HF=EF.
(3)过点O作ON⊥DE,OM⊥AB垂足分别为N、M,连接OD、OE、OA、OB.
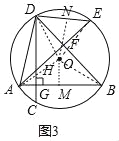
∴BM=![]() AB=4,
AB=4,
∵DH=DE=6,HF=EF,
∴DF⊥AE,
∴∠DAE+∠BDA=90°,
∵∠E O D=2∠DAE∠AO B=2∠ADB,
∴∠BOA+∠EOD=180°,
∵∠DOE=2∠NOE∠AOB=2∠BOM,
∴∠NOE+∠BOM=90°∠NOE+∠NEO=90°,
∵∠NEO=∠BOM,OE=OB,
∴△NOE≌△MBO
∴NE=OM=3,
∴OB=![]() =5,
=5,
∵∠ADB=∠BOM,
∴∠DAF=∠OBM,
在RT△OMB中sin∠OBM=![]() =
=![]()
∴sin∠DAE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0, a),C(b,0)满足
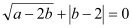 。
。(1)则C点的坐标为__________;A点的坐标为__________.
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.AC的中点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使
 ,若存在,请求出t的值;若不存在,请说明理由.
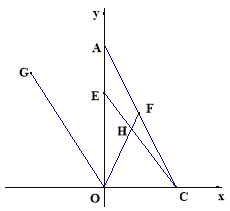
,若存在,请求出t的值;若不存在,请说明理由.(3)点F是线段AC上一点,满足∠FOC=∠FCO, 点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H, 当点E在线段OA上运动的过程中,
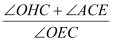 的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.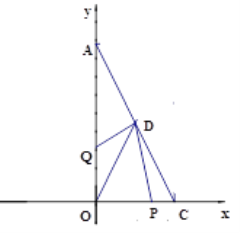
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张作纪念,全班共送了2070张相片.若全班有x名学生,根据题意,列出方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某钢铁厂去年1月份某种钢的产量为5000吨,3月份上升到7200吨,设平均每月的增长率为x,根据题意,得( )
A.5000(1+x2)=7200
B.5000(1+x)+5000(1+x)2=7200
C.5000(1+x)2=7200
D.5000+5000(1+x)+5000(1+x)2=7200 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解x3+2x2y+xy2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A和∠B互为补角,并且∠A的2倍比∠B小30°,求∠A和∠B.
相关试题

