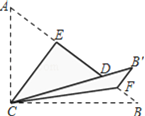
【题目】如图, 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为__________
参考答案:
【答案】![]()
【解析】试题分析:根据折叠的性质可知CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,
∴B′D=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC=![]() ACBC=
ACBC=![]() ABCE,
ABCE,
∴ACBC=ABCE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,
,
∴EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
∴DF=EF﹣ED=![]() ,
,
∴B′F=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设A、P两点间的距离为x.
探究:
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应x的值;如果不可能,试说明理由.
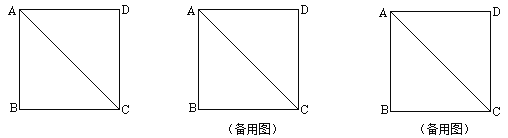
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣1)2+3的顶点坐标为( )
A.(2,1)
B.(2,﹣1)
C.(﹣1,3)
D.(1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣2(x+1)2+3的顶点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
A. 6.75×103吨 B. 6.75×104吨 C. 0.675×105吨 D. 67.5×103吨
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
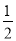
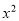 ﹣
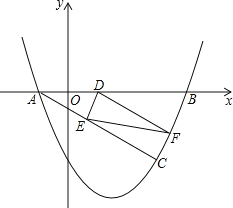
﹣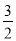 x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
x﹣2图象与x轴相交于A,B两点(点A在点B的左侧).若C(m,1﹣m)是抛物线上位于第四象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.(1)、求点A和点B的坐标;
(2)、求证:四边形DECF是矩形;
(3)、连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式加上3x2y﹣3xy2得x3﹣3x2y,则这个多项式是( )
A.x3+3xy2
B.x3﹣3xy2
C.x3﹣6x2y+3xy2
D.x3﹣6x2y﹣3x2y
相关试题

