【题目】如图,正方形OABC的顶点O在坐标原点,且OA边和AB边所在直线的解析式分别为:![]() 和
和![]() .
.
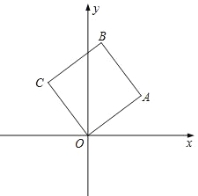
(1)求正方形OABC的边长;
(2)现有动点P、Q分别从C、A同时出发,点P沿线段CB向终点B运动,速度为每秒1个单位,点Q沿折线A→O→C向终点C运动,速度为每秒k个单位,设运动时间为2秒.当k为何值时,将△CPQ沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形?
(3)若正方形以每秒![]() 个单位的速度沿射线AO下滑,直至顶点C落在x轴上时停止下滑.设正方形在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
个单位的速度沿射线AO下滑,直至顶点C落在x轴上时停止下滑.设正方形在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
参考答案:
【答案】(1)5;(2)k=2或k=4;(3)![]() .
.
【解析】
试题分析:(1)联立方程组求得点A的坐标即可得到结果;
(2)有两种情况:①Q在OA上,则CQ=PQ时能构成菱形,根据题意列出2k=4即可求得;②Q点在OC上,则PC=QC时才能构成菱形,根据题意列出2k=8即可求得;
(3)①当点A运动到点O时,t=3,当0<t≤3时,设O′C′交x轴于点D,根据三角函数的定义tan∠DOO′=![]() ,即
,即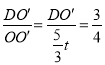 ,求得DO′=
,求得DO′=![]() t即可得到S=
t即可得到S=![]() DO′OO′=
DO′OO′=![]()
![]() t
t![]() t=
t=![]() t2;②当点C运动到x轴上时,t=(5×
t2;②当点C运动到x轴上时,t=(5×![]() )÷
)÷![]() =4,当3<t≤4时,设A′B′交x轴于点E由于A′O=
=4,当3<t≤4时,设A′B′交x轴于点E由于A′O=![]() t-5,于是得到A′E=
t-5,于是得到A′E=![]() A′O=
A′O=![]() 即可得到S=
即可得到S=![]() (A′E+O′D)A′O′=
(A′E+O′D)A′O′=![]() (
(![]() +
+![]() t)5=
t)5=![]() .
.
试题解析:(1)联立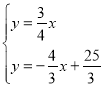 ,解得
,解得![]() ,
,
∴A(4,3),
∴OA=![]() ,
,
∴正方形OABC的边长为5;
(2)有两种情况:
①Q在OA上,则CQ=PQ时能构成菱形,
∵PC=2,
∴AQ=4时才能构成CQ=PQ的等腰三角形,
∴2k=4,解得k=2,
②Q点在OC上,∵∠PCQ是直角,
∴只有沿这PQ边对折才能构成菱形,且PC=QC,
∵
∴QC=2,
∴2k=OA+OC-QC=5+5-2=8,
∴k=4,
∴当k=2或k=4时将△CPQ沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形;
(3)①当点A运动到点O时,t=3,
当0<t≤3时,设O′C′交x轴于点D,
则tan∠DOO′=![]() ,即
,即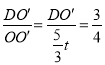 ,
,
∴DO′=![]() t,
t,
∴S=![]() DO′OO′=
DO′OO′=![]()
![]() t
t![]() t=
t=![]() t2,
t2,
②当点C运动到x轴上时,t=(5×![]() )÷
)÷![]() =4,
=4,
当3<t≤4时,设A′B′交x轴于点E,
∵A′O=![]() t-5,
t-5,
∴A′E=![]() A′O=
A′O=![]() ,
,
∴S=![]() (A′E+O′D)A′O′=
(A′E+O′D)A′O′=![]() (A′E+O′D)A′O′=
(A′E+O′D)A′O′=![]() (
(![]() +
+![]() t)5=
t)5=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+1,m+3)在直角坐标系的x轴上,则点P的坐标为( )
A.(0,2)
B.(﹣2,0)
C.(4,0)
D.(0,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】若x1,x2是一元二次方程x2+x﹣2=0的两个实数根,则x1+x2+x1x2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…则正方形OB2015B2016C2016的顶点B2016的坐标是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同.
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是 ;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率.(请利用树状图或列表法说明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会关注.“寒假”期间,记者小刘随机调查了某区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
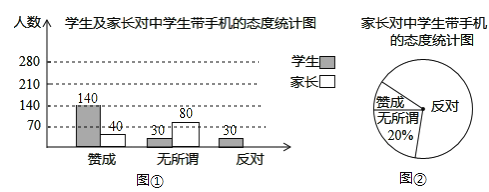
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)若该区共有中学生8000人,请根据以上图表信息估算出该区中学生中对“校园手机”持“无所谓”态度的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,且c为有理数,则ac2 ______ bc2.
相关试题

