【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 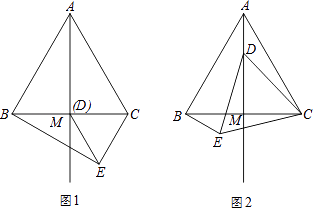
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
参考答案:
【答案】
(1)30
(2)解:(1)中结论成立.理由如下:
如图2.
∵△ABC和△CDE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE=60°,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
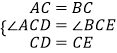 ,
,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵在等边△ABC中,M是BC中点.
∴∠CAD= ![]() ∠BAC=30°,
∠BAC=30°,
∴∠CBE=30°
(3)解:如图1.
∵在等边△ABC中,AB=6,
∴BC=AB=6.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴CD=BD= ![]() BC=3,
BC=3,
∵△CDE是等边三角形,
∴CE=CD=3.
【解析】解:(1)如图1.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=CD,
∵△CDE是等边三角形,
∴∠CDE=60°,CD=DE,
∴BD=DE,
∴∠BED=∠DBE,
又∵∠BED+∠DBE=∠CDE=60°,
∴∠DBE=30°,即∠CBE=30°;
所以答案是30;
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-14-(1-7)÷3×[(―3)2-3]
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市八年级8000名学生的体重情况,从中抽查了500名学生的体重进行统计分析,在这个问题中,样本容量是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
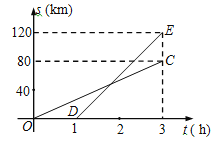
A. 乙到达B地时甲距A地120km. B. 乙出发1.8小时被甲追上.
C. 甲,乙相距20km时,t为2.4h. D. 甲的速度是乙的速度的
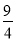 倍.
倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】基本事实:若am=an(a>0且a≠1,m、n是正整数),则m=n.试利用上述基本事实分别求下列各等式中x的值:①2×8x=27; ②2x+2+2x+1=24.
-
科目: 来源: 题型:
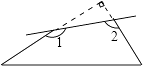
查看答案和解析>>【题目】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=度.
相关试题

