【题目】基本事实:若am=an(a>0且a≠1,m、n是正整数),则m=n.试利用上述基本事实分别求下列各等式中x的值:①2×8x=27; ②2x+2+2x+1=24.
参考答案:
【答案】解:①原方程可化为,2×23x=27 ,
∴23x+1=27 ,
3x+1=7,
解得x=2;
②原方程可化为,2×2x+1+2x+1=24,
∴2x+1(2+1)=24,
∴2x+1=8,
∴x+1=3,
解得x=2.
【解析】①先化为同底数幂相乘,再根据指数相等列出方程求解即可;
②先把2x+2化为2×2x+1 , 然后求出2x+1的值为8,再进行计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE.
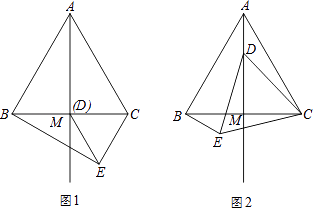
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
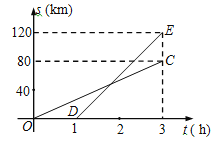
A. 乙到达B地时甲距A地120km. B. 乙出发1.8小时被甲追上.
C. 甲,乙相距20km时,t为2.4h. D. 甲的速度是乙的速度的
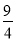 倍.
倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=度.
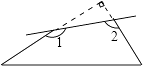
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把△ABC经过平移得到△A′B′C′,若A(1,m),B(4,2),点A的对应点A′(3,m+2),则点B对应点B′的标为( )
A.(6,5)
B.(6,4)
C.(5,m)
D.(6,m) -
科目: 来源: 题型:
查看答案和解析>>【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
相关试题

