【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是 ;
(3)当n=2时,先从袋中任意摸出1个球不放回,再从袋中任意摸出1个球,请用列表或画树状图的方法,求两次都摸到白球的概率.
参考答案:
【答案】(1)摸到红球和摸到白球的可能性相同;
(2)2;
(3)
两次摸出的球颜色不同的概率=![]() =
=![]() .
.
【解析】
试题分析:(1)当n=1时,利用概率公式可得到摸到红球和摸到白球的概率都为![]() ;
;
(2)利用频率估计概率,则摸到绿球的概率为0.25,根据概率公式得到![]() =0.25,然后解方程即可;
=0.25,然后解方程即可;
(3)先画树状图展示所有12种等可能的结果数,再找出两次摸出的球颜色不同的结果数,然后根据概率公式求解.
试题解析:(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性相同;
(2)利用频率估计概率得到摸到绿球的概率为0.25,
则![]() =0.25,解得n=2,
=0.25,解得n=2,
故答案为2;
(3)解:画树状图为:

共有12种等可能的结果数,其中两次摸出的球都是的结白色的结果共有2 种,
所以两次摸出的球颜色不同的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,观察图象,回答问题:
(1)点D的纵坐标等于____.
(2)点A的横坐标是方程______的解.
(3)大于点B横坐标的x的值是不等式________的解.
(4)点C的横、纵坐标是方程组_________的解.
(5)小于点C横坐标的x的值是不等式__________的解.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明今年的年龄是13岁,小华的年龄的3倍比小明的2倍多10岁,如果设小华的年龄为x岁,那么可以得到方程:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.绝对值相等的两数差为零
B.零减去一个数得这个数的相反数
C.两个有理数相减,就是把它们的绝对值相减
D.零减去一个数仍得这个数 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,对称轴条数最多的是( )
A. 正方形 B. 长方形 C. 等边三角形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=( )
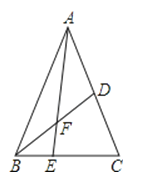
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个正比例函数的图象和一个一次函数的图象交于点A(-1,2),一次函数的图象交x轴负半轴于点B,且△AOB的面积为5,求这两个函数的表达式.
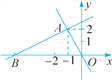
相关试题

