【题目】如图,直线 CB 和射线 OA,CB//OA,点 B 在点 C 的右侧.且满足∠OCB=∠OAB=100°,连接线段 OB,点 E、F 在直线 CB 上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE
(2)当点 E、F 在线段 CB 上时(如图 1),∠OEC 与∠OBA 的和是否是定值?若是,求出这个值;若不是,说明理由。
(3)如果平行移动 AB,点 E、F 在直线 CB 上的位置也随之发生变化.当点 E、F 在点 C 左侧时,∠OEC 和∠OBA 之间的数量关系是否发生变化?若不变,说明理由;若变化,求出他们之间的关系式.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(2)变化,
;(2)变化,![]() .
.
【解析】
(1)根据两直线平行,同旁内角互补求出![]() ,然后根据已知可得
,然后根据已知可得![]() ,由此计算即可得解;
,由此计算即可得解;
(2)根据两直线平行,同旁内角互补求出![]() ,再根据三角形的一个外角等于与它不相邻的两个内角的和可得
,再根据三角形的一个外角等于与它不相邻的两个内角的和可得![]() ,从而可得
,从而可得![]() ,由此即可解题;
,由此即可解题;
(3)同理(1)可得![]() ,根据三角形的内角和定理可知
,根据三角形的内角和定理可知![]() ,从而得到
,从而得到![]() ,由此计算即可得解.
,由此计算即可得解.
解:(1)![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
由(1)可知![]() ;
;
∴![]()
(3)变化,![]() ,
,
证明:当点 E、F 在点 C 左侧时,如图,

![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ;
;
∴![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
即:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
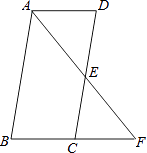
(1)求证:△ADE和△CEF的面积相等;
(2)若AB=2AD,试说明AF恰好是∠BAD的平分线. -
科目: 来源: 题型:
查看答案和解析>>【题目】足球是世界第一运动,参与足球运动可以锻炼身体,陶冶情操.“高新美少年,阳春蹴鞠忙”,让学生走出教室,走进阳光,让每一位学生健康、快乐成长,是高新一中初中校区一直秉承的理念.本月,我校第四届校园足球联赛落下了帷幕,并取得了四满成功.为了举办本次活动,我校在商场购买甲、乙两种不同的足球,购买甲种足球共花费2600元,购买乙种足球共花费1328元,购买甲种足球的数量是购买乙种足球数量的2.5倍,且购买一个乙种足球比购买一个甲种足球多花18元.求购买一个甲种足球、一个乙种足球各需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.
(1)求证:四边形CFAD为平行四边形.
(2)若∠BAC=90°,AB=4,BD=
 ,请求出四边形CFAD的面积.
,请求出四边形CFAD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③
 (∠α+∠β);④
(∠α+∠β);④ (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图(1),连接AF、CE.
①四边形AFCE是什么特殊四边形?说明理由;
②求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.

相关试题

