【题目】如图,在平面直角坐标系中,矩形OABC的边OA=2,OC=6,在OC上取点D将△AOD沿AD翻折,使O点落在AB边上的E点处,将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动,且一直角边始终经过点D,另一直角边所在直线与直线DE,BC分别交于点M,N.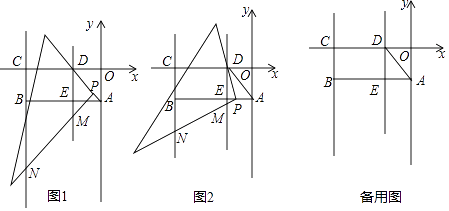
(1)填空:经过A,B,D三点的抛物线的解析式是;
(2)已知点F在(1)中的抛物线的对称轴上,求点F到点B,D的距离之差的最大值;
(3)如图1,当点P在线段DA上移动时,是否存在这样的点M,使△CMN为等腰三角形?若存在,请求出M点坐标;若不存在,请说明理由;
(4)如图2,当点P在线段AB上移动时,设P点坐标为(x,﹣2),记△DBN的面积为S,请直接写出S与x之间的函数关系式,并求出S随x增大而增大时所对应的自变量x的取值范围.
参考答案:
【答案】
(1)y=﹣ ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:∵点A,B关于抛物线的对称轴对称,
∴FA=FB,
∴|FB﹣FD|=|FA﹣FD|,
∵|FA﹣FD|≤AD=2 ![]() ,
,
∴点F到点B,D的距离之差的最大值是2 ![]() ;
;
(3)
解:存在点M使△CMN为等腰三角形,理由如下:
由翻折可知四边形AODE为正方形,过M作MH⊥BC于H,
∵∠PDM=∠PMD=45°,则∠NMH=∠MNH=45°,NH=MH=4,MN=4 ![]() ,
,
∵直线OE的解析式为:y=x,依题意得MN∥OE,∴设MN的解析式为y=x+b,
而DE的解析式为x=﹣2,BC的解析式为x=﹣6,
∴M(﹣2,﹣2+b),N(﹣6,﹣6+b),CM2=42+(﹣2+b)2,CN2=(﹣6+b)2,MN2=(4 ![]() )2=32,
)2=32,
①当CM=CN时,42+(﹣2+b)2=(﹣6+b)2,解得:b=2,此时M(﹣2,0);
②当CM=MN时,42+(﹣2+b)2=32,解得:b1=﹣2,b2=6(不合题意舍去),此时M(﹣2,﹣4);
③当CN=MN时,6﹣b=4 ![]() ,解得:b=﹣4
,解得:b=﹣4 ![]() +6,此时M(﹣2,4﹣4
+6,此时M(﹣2,4﹣4 ![]() );
);
综上所述,使△CMN为等腰三角形的M点的坐标为:(﹣2,0),(﹣2,﹣4),(﹣2,4﹣4 ![]() );
);
(4)
解:当﹣2≤x≤0时,∵∠BPN+∠DPE=90°,∠BPN+∠BNP=90°,
∴∠DPE=∠BNP,又∠PED=∠NBP=90°,
∴△DEP∽△PBN,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BN= ![]() ,
,
∴S△DBN= ![]() BN×BE=
BN×BE= ![]() ×
× ![]() ×4,整理得:S=x2+8x+12;
×4,整理得:S=x2+8x+12;
当﹣6≤x<﹣2时,
∵△PBN∽△DEP,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BN= ![]() ,
,
∴S△DBN= ![]() BN×BE=
BN×BE= ![]() ×
× ![]() ×4,整理得:S=﹣x2﹣8x﹣12;
×4,整理得:S=﹣x2﹣8x﹣12;
则S与x之间的函数关系式:S= ![]() ,
,
①当﹣2≤x≤0时,S=x2+8x+12=(x+4)2﹣4,当x≥﹣4时,S随x的增大而增大,即﹣2≤x≤0,
②当﹣6≤x<﹣2时,S=﹣x2﹣8x﹣12=﹣(x+4)2+4,当x≤﹣4时,S随x的增大而增大,即﹣6≤x≤﹣4,
综上所述:S随x增大而增大时,﹣2≤x≤0或﹣6≤x≤﹣4.
【解析】解:(1)设抛物线解析式为y=ax2+bx+c(a≠0),
∵将△AOD沿AD翻折,使O点落在AB边上的E点处,
∴∠OAD=∠EAD=45°,DE=OD,
∴OA=OD,
∵OA=2,
∴OD=2,
∴D点坐标是(2,0),
把A(0,﹣2),B(﹣6,﹣2),D(2,0)分别代入y=ax2+bx+c(a≠0),得 ,解得
,解得 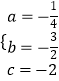 ,
,
故抛物线解析式为:y=﹣ ![]() x2﹣
x2﹣ ![]() x﹣2.
x﹣2.
故答案是:y=﹣ ![]() x2﹣
x2﹣ ![]() x﹣2;
x﹣2;
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,四边形ABCD中,∠A=106°
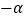 , ∠ABC=74°
, ∠ABC=74°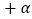 ,BD⊥DC于点D, EF⊥DC于点F.
,BD⊥DC于点D, EF⊥DC于点F.求证:∠1=∠2.

证明: ∵∠A=106°
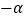 ,∠ABC=74°
,∠ABC=74°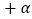 (已知)
(已知)∴∠A+∠ABC=180°
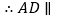 ( )
( )∴∠1=
∵BD⊥DC,EF⊥DC (已知)
∴∠BDF=∠EFC=90°( )
∴BD∥ ( )
∴∠2= ( )
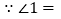 (已证)
(已证)∴∠1=∠2 ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=α,点P是∠MON角平分线上一点,点A在射线OM上,作∠APB=180°-α,交直线ON于点B,PC⊥ON于C.
(1)如图1,若∠MON=90°时,求证:PA=PB;
(2)如图2,若∠MON=60°时,写出线段OB,OA及BC之间的数量关系,并说明理由;
(3)如图3,若∠MON=60°时,点B在射线ON的反向延长线上时,(2)中结论还成立吗?若不成立,直接写出线段OB,OA及BC之间的数量关系(不需要证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】校园安全与每个师生、家长和社会有着切身的关系.某校教学楼共五层,设有左、右两个楼梯口,通常在放学时,若持续不正常,会导致等待通过的人较多,发生拥堵,从而出现不安全因素.通过观察发现位于教学楼二、三楼的七年级学生从放学时刻起,经过单个楼梯口等待人数按每分钟12人递增,6分钟后经过单个楼梯口等待人数按每分钟12人递减;位于四、五楼的八年级学生从放学时刻起,经过单个楼梯口等待人数y2与时间为t(分)满足关系式y2=﹣4t2+48t﹣96(0≤t≤12).若在单个楼梯口等待人数超过80人,就会出现安全隐患.
(1)试写出七年级学生在单个楼梯口等待的人数y1(人)和从放学时刻起的时间t(分)之间的函数关系式,并指出t的取值范围.
(2)若七、八年级学生同时放学,试计算等待人数超过80人所持续的时间.
(3)为了避免出现安全隐患,该校采取让七年级学生提前放学措施,要使单个楼梯口等待人数不超过80人,则七年级学生至少比八年级提前几分钟放学? -
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织了一次读书活动,统计了16名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这16名同学一周内累计读书时间的中位数是 .
一周内累计的读书时间(小时)
5
8
10
14
人数(个)
1
7
5
3
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣2,﹣1,0,1,3,4这七个数中随机抽取一个数记为a,a的值既是不等式组
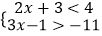 的解,又在函数y=
的解,又在函数y= 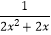 的自变量取值范围内的概率是 .
的自变量取值范围内的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数
 、
、 我们定义一种新运算
我们定义一种新运算 (其中
(其中 、
、 均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为
均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为 ,其中
,其中 、
、 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数 、
、 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的 、
、 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.(1)若
 ,则
,则
 .
.(2)已知
 ,若正格线性数
,若正格线性数 ,求满足不等式组
,求满足不等式组 的所有
的所有 的值.
的值.
相关试题

