【题目】校园安全与每个师生、家长和社会有着切身的关系.某校教学楼共五层,设有左、右两个楼梯口,通常在放学时,若持续不正常,会导致等待通过的人较多,发生拥堵,从而出现不安全因素.通过观察发现位于教学楼二、三楼的七年级学生从放学时刻起,经过单个楼梯口等待人数按每分钟12人递增,6分钟后经过单个楼梯口等待人数按每分钟12人递减;位于四、五楼的八年级学生从放学时刻起,经过单个楼梯口等待人数y2与时间为t(分)满足关系式y2=﹣4t2+48t﹣96(0≤t≤12).若在单个楼梯口等待人数超过80人,就会出现安全隐患.
(1)试写出七年级学生在单个楼梯口等待的人数y1(人)和从放学时刻起的时间t(分)之间的函数关系式,并指出t的取值范围.
(2)若七、八年级学生同时放学,试计算等待人数超过80人所持续的时间.
(3)为了避免出现安全隐患,该校采取让七年级学生提前放学措施,要使单个楼梯口等待人数不超过80人,则七年级学生至少比八年级提前几分钟放学?
参考答案:
【答案】
(1)解:由题意得,y1= ![]() ;
;
(2)解:同时放学:七年级单个楼梯口等待人数为y= ![]() ,
,
当0≤t≤6时,﹣4t2+60t﹣96=80,得t1=4,t2=11,
∴4≤t≤6;
当6<t≤12时,﹣4t2+36t+48=80,得t1=1,t2=8,
∴6<t≤8.
∵8﹣4=4,
∴等待人数超过80人所持续的时间为:8﹣4=4(分).
∴等待人数超过80人所持续的时间为:8﹣4=4分钟;
(3)解:设七年级学生比八年级提前m(m>0)分钟放学,
当0≤t≤6﹣m时,y=﹣4t2+48t﹣96+12(t+m)=﹣4t2+60t+12m﹣96,
∵﹣ ![]() =7.5>6﹣m,
=7.5>6﹣m,
∴当t=6﹣m时,y有最大值=﹣4m2+120,由﹣4m2+120≤80,
∵m>0,
∴m2≥10,得m≥ ![]() ;
;
当6﹣m<t≤12﹣m时,y=﹣4t2+48t﹣96+144﹣12(t+m)=﹣4t2+36t﹣12m+48,
∵﹣ ![]() =4.5,
=4.5,
∴当t=4.5时,y有最大值=129﹣12m≤80,得m≥4 ![]() ;
;
当12﹣m<t≤12时,y=﹣4t2+48t﹣96=﹣4(t﹣6)2+48≤48.
∴要使单个楼梯口等待人数不超过80人,则七年级学生比八年级至少提前4 ![]() 分钟放学,
分钟放学,
【解析】(1)前六分钟时,七年级单个楼梯口等待人数=12×时间;6分钟后七年级单个楼梯口等待人数=6×12﹣12×超过6分钟的时间,注意应根据等待的人数为非负数得到自变量的取值;(2)根据同时放学4、5楼不变,但2、3楼需要加八年级的人数,从而得出关系式求出即可;(3)让(1)(2)得到的式子为80列式求值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据
 ≈1.41,
≈1.41,  ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,四边形ABCD中,∠A=106°
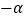 , ∠ABC=74°
, ∠ABC=74°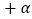 ,BD⊥DC于点D, EF⊥DC于点F.
,BD⊥DC于点D, EF⊥DC于点F.求证:∠1=∠2.

证明: ∵∠A=106°
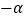 ,∠ABC=74°
,∠ABC=74°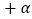 (已知)
(已知)∴∠A+∠ABC=180°
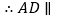 ( )
( )∴∠1=
∵BD⊥DC,EF⊥DC (已知)
∴∠BDF=∠EFC=90°( )
∴BD∥ ( )
∴∠2= ( )
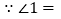 (已证)
(已证)∴∠1=∠2 ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=α,点P是∠MON角平分线上一点,点A在射线OM上,作∠APB=180°-α,交直线ON于点B,PC⊥ON于C.
(1)如图1,若∠MON=90°时,求证:PA=PB;
(2)如图2,若∠MON=60°时,写出线段OB,OA及BC之间的数量关系,并说明理由;
(3)如图3,若∠MON=60°时,点B在射线ON的反向延长线上时,(2)中结论还成立吗?若不成立,直接写出线段OB,OA及BC之间的数量关系(不需要证明).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA=2,OC=6,在OC上取点D将△AOD沿AD翻折,使O点落在AB边上的E点处,将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动,且一直角边始终经过点D,另一直角边所在直线与直线DE,BC分别交于点M,N.
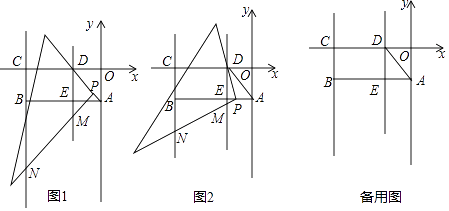
(1)填空:经过A,B,D三点的抛物线的解析式是;
(2)已知点F在(1)中的抛物线的对称轴上,求点F到点B,D的距离之差的最大值;
(3)如图1,当点P在线段DA上移动时,是否存在这样的点M,使△CMN为等腰三角形?若存在,请求出M点坐标;若不存在,请说明理由;
(4)如图2,当点P在线段AB上移动时,设P点坐标为(x,﹣2),记△DBN的面积为S,请直接写出S与x之间的函数关系式,并求出S随x增大而增大时所对应的自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织了一次读书活动,统计了16名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这16名同学一周内累计读书时间的中位数是 .
一周内累计的读书时间(小时)
5
8
10
14
人数(个)
1
7
5
3
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣2,﹣1,0,1,3,4这七个数中随机抽取一个数记为a,a的值既是不等式组
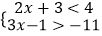 的解,又在函数y=
的解,又在函数y= 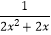 的自变量取值范围内的概率是 .
的自变量取值范围内的概率是 .
相关试题

