【题目】某新建成学校举行美化绿化校园活动,九年级计划购买![]() ,
,![]() 两种花木共100棵绿化操场,其中
两种花木共100棵绿化操场,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若购进![]() ,
,![]() 两种花木刚好用去8000元,则购买了
两种花木刚好用去8000元,则购买了![]() 两种花木各多少棵?
两种花木各多少棵?
(2)如果购买![]() 花木的数量不少于
花木的数量不少于![]() 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
参考答案:
【答案】(1)购买A种花木40棵,B种花木60棵;(2)当购买A种花木50棵、B种花木50棵时,所需总费用最低,最低费用为7500元.
【解析】
试题分析:(1)设购买A种花木x棵,B种花木y棵,根据“A,B两种花木共100棵、购进A,B两种花木刚好用去8000元”列方程组求解可得;
(2)设购买A种花木a棵,则购买B种花木(100﹣a)棵,根据“B花木的数量不少于A花木的数量”求得a的范围,再设购买总费用为W,列出W关于a的解析式,利用一次函数的性质求解可得.
试题解析:(1)设购买A种花木x棵,B种花木y棵,
根据题意,得:![]() ,解得:
,解得:![]() ,
,
答:购买A种花木40棵,B种花木60棵;
(2)设购买A种花木a棵,则购买B种花木(100﹣a)棵,
根据题意,得:100﹣a≥a,解得:a≤50,
设购买总费用为W,则W=50a+100(100﹣a)=﹣50a+10000,
∵W随a的增大而减小,∴当a=50时,W取得最小值,最小值为7500元,
答:当购买A种花木50棵、B种花木50棵时,所需总费用最低,最低费用为7500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面调查适合利用选举的形式进行数据收集的是( )
A. 谁在电脑福利彩票中中一等奖
B. 10月1日是什么节日
C. 谁在某地2013年中考中取得第一名
D. 谁最适合当文艺委员
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的宽为xcm,长比宽多2cm,面积为scm2.
(1)求s与x之间的函数关系式;
(2)当x=8时,长方形的面积为多少cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级二班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结
束后,该班植树情况的部分统计图如下所示,那么该班的总人数是 人.
-
科目: 来源: 题型:
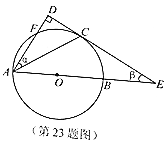
查看答案和解析>>【题目】如图,
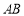 是
是 的直径,
的直径,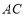 是上半圆的弦,过点
是上半圆的弦,过点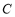 作
作 的切线
的切线 交
交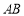 的延长线于点
的延长线于点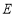 ,过点
,过点 作切线
作切线 的垂线,垂足为
的垂线,垂足为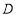 ,且与
,且与 交于点
交于点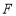 ,设
,设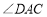 ,
, 的度数分别是
的度数分别是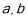 .
.
(1)用含
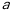 的代数式表示
的代数式表示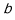 ,并直接写出
,并直接写出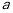 的取值范围;
的取值范围;(2)连接
 与
与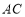 交于点
交于点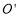 ,当点
,当点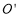 是
是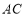 的中点时,求
的中点时,求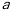 ,
,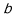 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】规定:对于任意实数a,b都有:a⊕b=a(a-b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2-5)+1=2×(-3)+1=-5,那么等式3⊕x=16的解是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中有一个黑球
 和两个白球
和两个白球 (除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(除颜色外其他均相同).用树状图(或列表法)解答下列问题:(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球,则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
相关试题

