【题目】如图,已知∠ABC+∠ECB=180°,∠P=∠Q,

(1)AB与ED平行吗?为什么?
(2)PB与CD平行吗?为什么?
(3)∠1与∠2是否相等?说说你的理由.
参考答案:
【答案】(1)AB∥ED(2)BP∥CD(3)∠1=∠2
【解析】
(1)根据同旁内角互补,两直线平行即可得出结论;
(2)根据内错角相等,两直线平行即可得出结论
(3)由AB∥CD,则∠ABC=∠BCD,再由∠P=∠Q,则∠PBC=∠QCB,从而得出∠1=∠2.
(1)AB∥ED,理由如下,
∵∠ABC+∠ECB=180°,
∴AB∥ED(同旁内角互补,两直线平行可得);
(2)BP∥CD,理由如下,
∵∠P=∠Q,
∴BP∥CQ(内错角相等,两直线平行),
(3)∠1=∠2,理由如下,
∵AB∥CD,
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵BP∥CQ(已证),
∴∠PBC=∠QCB(两直线平行,内错角相等),
∴∠ABC-∠PBC=∠BCD-∠QCB
即∠1=∠2.
-
科目: 来源: 题型:
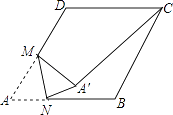
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 (x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣
(x+2)(x﹣4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣  x+b与抛物线的另一交点为D.
x+b与抛物线的另一交点为D.
(1)若点D的横坐标为﹣5,求抛物线的函数表达式;
(2)若在第一象限内的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求k的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

-
科目: 来源: 题型:
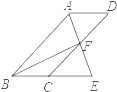
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: ﹣4sin30°+(2014﹣π)0﹣22 .
﹣4sin30°+(2014﹣π)0﹣22 .
(2)解不等式组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.

(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
相关试题

