【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
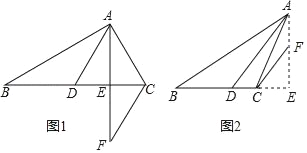
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
参考答案:
【答案】(1)20;(2)![]() y﹣
y﹣![]() x;(3)(2)中的结论成立.
x;(3)(2)中的结论成立.
【解析】
(1)求∠CFE的度数,求出∠DAE的度数即可,只要求出∠BAE-∠BAD的度数,由平分和垂直易得∠BAE和∠BAD的度数即可;
(2)由(1)类推得出答案即可;
(3)类比以上思路,把问题转换为∠CFE=90°-∠ECF解决问题.
解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°﹣∠B﹣∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,
∵CF∥AD,
∴∠CFE=∠DAE=20°;
故答案为:20;
(2)∵∠BAE=90°﹣∠B,∠BAD=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠BCA),
(180°﹣∠B﹣∠BCA),
∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣![]() (180°﹣∠B﹣∠BCA)=
(180°﹣∠B﹣∠BCA)=![]() (∠BCA﹣∠B)=
(∠BCA﹣∠B)=![]() y﹣
y﹣![]() x.
x.
故答案为:![]() y﹣
y﹣![]() x;
x;
(3)(2)中的结论成立.
∵∠B=x,∠ACB=y,
∴∠BAC=180°﹣x﹣y,
∵AD平分∠BAC,
∴∠DAC=![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() x﹣
x﹣![]() y,
y,
∵CF∥AD,
∴∠ACF=∠DAC=90°﹣![]() x﹣
x﹣![]() y,
y,
∴∠BCF=y+90°﹣![]() x﹣
x﹣![]() y=90°﹣
y=90°﹣![]() x+
x+![]() y,
y,
∴∠ECF=180°﹣∠BCF=90°+![]() x﹣
x﹣![]() y,
y,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°﹣∠ECF=![]() y﹣
y﹣![]() x.
x.
-
科目: 来源: 题型:
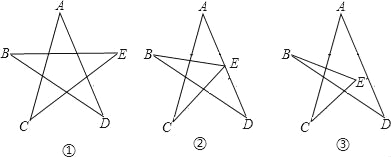
查看答案和解析>>【题目】如图①所示,为五角星图案,图②、图③叫做蜕变的五角星.试回答以下问
(1)在图①中,试证明∠A+∠B+∠C+∠D+∠E=180°;
(2)对于图②或图③,还能得到同样的结论吗?若能,请在图②或图③中任选其一证明你的发现;若不能,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A.
B.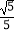
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )

A.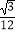
B.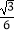
C.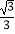
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( )
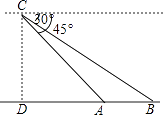
A.3000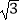 m
m
B.3000(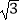 +1)m
+1)m
C.3000(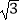 -1)m
-1)m
D.1500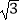 m
m -
科目: 来源: 题型:
查看答案和解析>>【题目】济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,
 ≈1.7,结果精确到1m,则该楼的高度CD为( )
≈1.7,结果精确到1m,则该楼的高度CD为( ) 
A.47m
B.51m
C.53m
D.54m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=
 ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
相关试题

