【题目】如图,在矩形ABCO中,AO=3,tan∠ACB=![]() ,以O为坐标原点,OC为
,以O为坐标原点,OC为![]() 轴,OA为
轴,OA为![]() 轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为
轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为![]() 秒。
秒。
(1)求直线AC的解析式;
(2)用含![]() 的代数式表示点D的坐标;
的代数式表示点D的坐标;
(3)当![]() 为何值时,△ODE为直角三角形?
为何值时,△ODE为直角三角形?
(4)在什么条件下,以Rt△ODE的三个顶点能确定一条对称轴平行于![]() 轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.
轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.

参考答案:
【答案】(1)![]() ;(2)D(
;(2)D(![]() ,
,![]() );(3)
);(3)![]() ,
,![]() ,
,![]() ,
,![]() ;(4)
;(4)![]()
【解析】
(1)在Rt△AOC中,已知AO的长以及∠ACB的正弦值,能求出OC的长,即可确定点C的坐标,利用待定系数法能求出直线AC的解析式.
(2)过D作AO、OC的垂线,通过构建相似三角形来求出点D的坐标.
(3)用t表示出OD、DE、OE的长,若△ODE为直角三角形,那么三边符合勾股定理,据此列方程求出对应的t的值.
(4)根据(3)的结论能得到t的值,△ODE中,当OD⊥x轴或DE垂直x轴时,都不能确定“一条对称轴平行于y轴的抛物线”,余下的情况都是符合要求的,首先得D、E的坐标,再利用待定系数法求出抛物线的解析式.
(1)根据题意,得CO=AB=BCtan∠ACB=4,则A(0,3)、B(4,3)、C(4,0);
设直线AC的解析式为:y=kx+3,代入C点坐标,得:
4k+3=0,k=-![]() ,
,
∴直线AC:![]() ;
;
(2)分别作DF⊥AO,DH⊥CO,垂足分别为F,H,
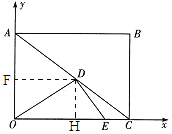
则有△ADF∽△DCH∽△ACO,
∴AD:DC:AC=AF:DH:AO=FD:HC:OC,
而AD=![]() (其中0≤
(其中0≤![]() ≤
≤![]() ),OC=AB=4,AC=5,∴FD=
),OC=AB=4,AC=5,∴FD=![]() AD=
AD=![]() ,AF=
,AF=![]() AD=
AD=![]() ,
,
DH=![]() ,HC=
,HC=![]() ,
,
∴D(![]() ,
,![]() );
);
(3)CE=![]() ,E(
,E(![]() ,0),OE=OC-CE=4-
,0),OE=OC-CE=4-![]() ,HE=|CH-CE|=
,HE=|CH-CE|=![]() ,
,
则OD2=DH2+OH2=![]() =
=![]() ,
,
DE2=DH2+HE2=![]() =
=![]() ,
,
当△ODE为Rt△时,有OD2+DE2=OE2,或OD2+OE2=DE2,或DE2+OE2=OD2,
即![]() ①,
①,
或![]() ②,
②,
或![]() ③,
③,
上述三个方程在0≤![]() ≤
≤![]() 内的所有实数解为
内的所有实数解为
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(4)当DO⊥OE,及DE⊥OE时,即![]() 和
和![]() 时,以Rt△ODE的三个顶点不确定对称轴平行于
时,以Rt△ODE的三个顶点不确定对称轴平行于![]() 轴的抛物线,其它两种情况都可以各确定一条对称轴平行于
轴的抛物线,其它两种情况都可以各确定一条对称轴平行于![]() 轴的抛物线D(
轴的抛物线D(![]() ,
,![]() ),E(4-
),E(4-![]() ,0),
,0),
当![]() 时,D(
时,D(![]() ,
,![]() ),E(3,0),因为抛物线过O(0,0),
),E(3,0),因为抛物线过O(0,0),
所以设所求抛物线为![]() ,将点D,E坐标代入,求得
,将点D,E坐标代入,求得![]() ,
,![]() ,
,
∴所求抛物线为![]() .
.
(当![]() 时,所求抛物线为
时,所求抛物线为![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
-
科目: 来源: 题型:
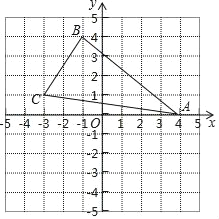
查看答案和解析>>【题目】如图,在直角坐标系中,△ABC各顶点的横、纵坐标都是整数,
(1)写出△ABC各顶点的坐标;
(2)作出△ABC关于x轴对称的图形△A1B1C1;
(3)写出△A1B1C1的各顶点关于y轴对称点A2,B2,C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块直角三角尺形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大.
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧
 的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
(1)求证:DE=DB;
(2)连接BE,试判断△ABE的形状,并说明理由.

相关试题

