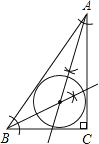
【题目】如图,一块直角三角尺形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大.
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.

参考答案:
【答案】(1)画图见解析; (2)100πcm 2.
【解析】
(1)可作出任意两个内角的平分线,交点即为所求的圆心,交点到任意边的距离为半径画圆即可;
(2)设三角形内切圆半径为r,由勾股定理得出AB=50,再根据三角形的面积等于周长乘以半径的一半,从而得出三角形内切圆半径.
(1)如图所示:
(2)设三角形内切圆半径为r,则![]() r(50+40+30)=
r(50+40+30)=![]() ×30×40,解得r=10(cm),
×30×40,解得r=10(cm),
故此圆凳面的面积为:π×102=100π(cm 2).
-
科目: 来源: 题型:
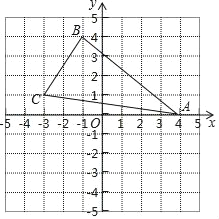
查看答案和解析>>【题目】如图,在直角坐标系中,△ABC各顶点的横、纵坐标都是整数,
(1)写出△ABC各顶点的坐标;
(2)作出△ABC关于x轴对称的图形△A1B1C1;
(3)写出△A1B1C1的各顶点关于y轴对称点A2,B2,C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCO中,AO=3,tan∠ACB=
 ,以O为坐标原点,OC为
,以O为坐标原点,OC为 轴,OA为
轴,OA为 轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为
轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为 秒。
秒。(1)求直线AC的解析式;
(2)用含
 的代数式表示点D的坐标;
的代数式表示点D的坐标;(3)当
 为何值时,△ODE为直角三角形?
为何值时,△ODE为直角三角形?(4)在什么条件下,以Rt△ODE的三个顶点能确定一条对称轴平行于
 轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.
轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧
 的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
(1)求证:DE=DB;
(2)连接BE,试判断△ABE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;(2)连接OF,OG,求∠OGF.

相关试题

