【题目】解下列各题（每题5分，共30分）

（1） （2）

（3） （4） 解不等式2（x+2）-6≤-5（x-4）

（5） （6）

参考答案：

【答案】（1）x=-15；（2）；（3）－4.5≤x＜1；

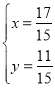（4）x≤；（5）；（6）.

【解析】

（1）根据解一元一次方程的方法步骤求解即可；

（2）用代入消元法或加减消元法求解；

（3）先解每个不等式的解集，再求其公共部分；

（4）根据解一元一次不等式的方法步骤求解；

（5）先化简方程组的两个方程，再用代入消元法或加减消元法求解；

（6）把x=3z代入后两个方程并化简，再解由y、z组成的二元一次方程组，即可求得原方程组的解.

解：（1）去分母得，

去括号得，，

移项化简得，，

即.

（2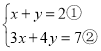），①×4－②，得，

把代入①得，，解得y=1，

所以方程组的解是.

（3），

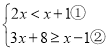解不等式①得，x＜1，

解不等式②得，x≥－4.5，

所以不等式组的解集是－4.5≤x＜1.

（4）2（x+2）－6≤－5（x－4）

去括号得，

移项化简得，

不等式两边同时除以7得，x≤.

（5）原方程组可化为：，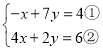

①×4+②得，，解得：；

把代入①，得，解得：.

所以原方程组的解是.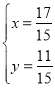

（6），

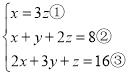把①代入②得，，即④，

把①代入③得，，即⑤，

解由④⑤组成的方程组得：，

把z=1代入①得，x=3；

所以原方程组的解是.

关闭