搜索
【题目】图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1.6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0.8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0.1m）． （参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）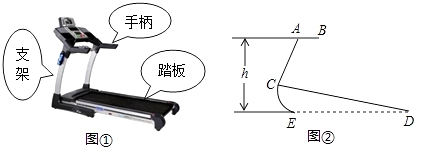
参考答案：
【答案】解：过C点作FG⊥AB于F，交DE于G．
∵CD与地面DE的夹角∠CDE为12°，∠ACD为80°，
∴∠ACF=∠FCD﹣∠ACD=∠CGD+∠CDE﹣∠ACD=90°+12°﹣80°=22°，
∴∠CAF=68°，
在Rt△ACF中，CF=ACsin∠CAF≈0.744m，
在Rt△CDG中，CG=CDsin∠CDE≈0.336m，
∴FG=FC+CG≈1.1m．
故跑步机手柄的一端A的高度约为1.1m．
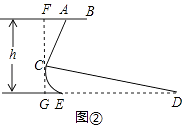
【解析】过C点作FG⊥AB于F，交DE于G．在Rt△ACF中，根据三角函数可求CF，在Rt△CDG中，根据三角函数可求CG，再根据FG=FC+CG即可求解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在读书月活动中，学校准备购买一批课外读物，为使课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图．
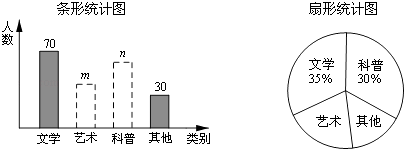
请你根据统计图提供的信息，解答下列问题：
（1）本次调查中，一共调查了多少名同学；
（2）条形统计图中，m，n的值；
（3）扇形统计图中，求出艺术类读物所在扇形的圆心角的度数；
（4）学校计划购买课外读物6000册，请根据样本数据，估计学校应购买其他类读物多少册？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，O为直线AB上一点，过点O作射线OC，
，将一直角三角板
的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．
将图1中的三角板绕点O以每秒
的速度沿逆时针方向旋转一周
如图2，经过t秒后，ON落在OC边上，则
______秒
直接写结果
．
如图2，三角板继续绕点O以每秒的速度沿逆时针方向旋转到起点OA上同时射线OC也绕O点以每秒
的速度沿逆时针方向旋转一周，
当OC转动9秒时，求
的度数．
运动多少秒时，
？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场举行开业酬宾活动，设立了两个可以自由转动的转盘（如图所示，两个转盘均被等分），并规定：顾客购买满188元的商品，即可任选一个转盘转动一次，转盘停止后，指针所指区域内容即为优惠方式；若指针所指区域空白，则无优惠．已知小张在该商场消费300元
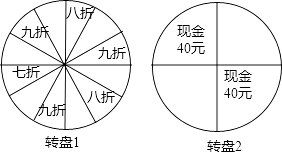
（1）若他选择转动转盘1，则他能得到优惠的概率为多少？
（2）选择转动转盘1和转盘2，哪种方式对于小张更合算，请通过计算加以说明． -
科目： 来源： 题型：
查看答案和解析>>【题目】规定两数a，b之间的一种运算，记作(a，b)：如果
，那么(a，b)=c．例如：因为23=8，所以(2，8)=3．
（1）根据上述规定，填空：
（3，27）=_______，（5，1）=_______，（2，
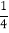
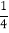）=_______．（2）小明在研究这种运算时发现一个现象：（3n，4n）=（3，4）小明给出了如下的证明：
设（3n，4n）=x，则（3n）x=4n，即（3x）n=4n
所以3x=4，即（3，4）=x，
所以（3n，4n）=（3，4）．
请你尝试运用这种方法证明下面这个等式：(3，4)+(3，5)=(3，20)
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个由若干小正方形堆成的几何体，它从正面看和从左面看的图形如图1所示．
这个几何体可以是图2中甲，乙，丙中的______；
这个几何体最多由______个小正方体堆成，最少由______个小正方体堆成；
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2008年北京奥运会后，同学们参与体育锻炼的热情高涨．为了解他们平均每周的锻炼时间，小明同学在校内随机调查了50名同学，统计并制作了如下的频数分布表和扇形统计图．根据上述信息解答下列问题：
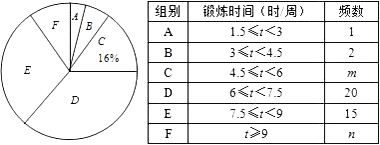
（1）m= ， n=；
（2）在扇形统计图中，D组所占圆心角的度数为度；
（3）全校共有3000名学生，估计该校平均每周体育锻炼时间不少于6小时的学生约有多少名？
相关试题
