【题目】有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.现要把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上.
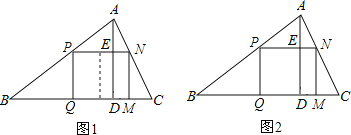
(1)如果此矩形可分割成两个并排放置的正方形,如图1,此时,这个矩形零件的两条邻边长分别为多少mm?请你计算.
(2)如果题中所要加工的零件只是矩形,如图2,这样,此矩形零件的两条邻边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条邻边长.
参考答案:
【答案】(1)这个矩形零件的两条边长分别为![]() mm,
mm,![]() mm;(2)S的最大值为2400mm2,此时PN=60mm,PQ=80﹣
mm;(2)S的最大值为2400mm2,此时PN=60mm,PQ=80﹣![]() ×60=40(mm).
×60=40(mm).
【解析】
试题分析:(1)由于矩形是由两个并排放置的正方形所组成,则可设PQ=ymm,则PN=2ymm,易证△APN∽△ABC,由相似三角形的性质解答即可;
(2)设PN=x,用PQ表示出AE的长度,然后根据相似三角形对应高的比等于相似比列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答
解:(1)设矩形的边长PN=2ymm,则PQ=ymm,
∵PN∥BC,
∴△APN∽△ABC,
∴![]() ,
,
即![]() ,
,
解得y=![]() ,
,
∴PN=![]() ×2=
×2=![]() (mm),
(mm),
答:这个矩形零件的两条边长分别为![]() mm,
mm,![]() mm;
mm;
(2)设PN=xmm,由条件可得△APN∽△ABC,
∴![]() ,
,
即![]() ,
,
解得PQ=80﹣![]() x.
x.
∴S=PNPQ=x(80﹣![]() x)=﹣
x)=﹣![]() x2+80x=﹣
x2+80x=﹣![]() (x﹣60)2+2400,
(x﹣60)2+2400,
∴S的最大值为2400mm2,此时PN=60mm,PQ=80﹣![]() ×60=40(mm).
×60=40(mm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
A. 正六边形 B. 正五边形 C. 正方形 D. 正三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批名牌衬衫,要求一等品的数量12850件左右,请问该商场应购进多少件这样的衬衫?下面是该部门经理随机抽查一些衬衫后,统计得到的一等品的频率变化表:
抽查数n
100
200
1500
2000
2500
一等品数m
94
1430
1902
一等品频率
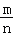
0.97
0.95
(1)把表格补充完整(结果保留两位小数);
(2)任意抽取1件衬衫,抽得一等品的概率约为多少?
(3)你能求得商场应购进多少件这样的衬衫吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市百万读书工程活动中,就我县中小学教师阅读状况进行了一次问卷调查,并根据调查结果绘制了教师每年阅读书籍数量的统计图(不完整),设x表示阅读书籍的数量(x为正整数,单位:本),其中A:1≤x≤3,B:4≤x≤6,C:7≤x≤9,D:x≥10.
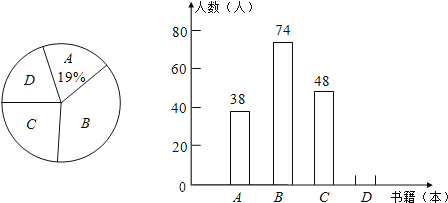
(1)本次共调查了 名教师;
(2)扇形统计图中扇形D的圆心角的度数为 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
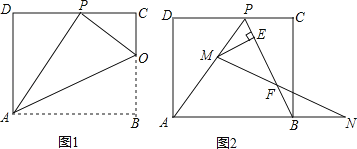
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,

 ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式中,正确的是( )
A. 3a﹣2a=1 B. a2a3=a5 C. (﹣2a3)2=﹣4a6 D. (a﹣b)2=a2﹣b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式
① -49a2bc-14ab2c+7ab
②(2a+b)(2a-3b)-8a(2a+b)
相关试题

