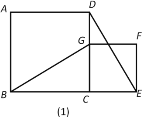
【题目】如图(1),正方形ABCD和正方形CEFG有一公共点C,且B,C,E在同一直线,连接BG,DE.
(1)请你猜想BG,DE的位置关系和数量关系,并说明理由.
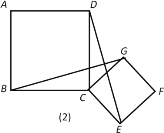
(2)若正方形CEFG绕点C按顺时针方向旋转一个角度后,如图(2),BG和DE是否还存在上述关系,并说明理由.
参考答案:
【答案】(1)BG⊥DE,BG=DE;(2)BG与DE仍具有上述关系,即BG⊥DE,BG=DE
【解析】
(1)由四边形ABCD,CEFG都是正方形,得到CB=CD,CG=CE,∠BCG=∠DCE=90°,于是Rt△BCG≌Rt△DCE,得到BG=DE,∠CBG=∠CDE,根据三角形内角和定理可得到∠DHG=∠GCB=90°,即BG⊥DE.
(2)BG和DE还有上述关系.证明的方法与(1)一样.
解:(1)BG⊥DE,BG=DE
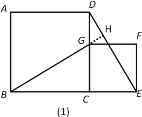
理由:如图(1),延长BG交DE于点H
∵四边形ABCD,CEFG都是正方形,
∴CB=CD,CG=CE,∠BCG=∠DCE=90°,
∴Rt△BCG≌Rt△DCE,
∴BG=DE,∠CBG=∠CDE,
而∠BGC=∠DGH,
∴∠DHG=∠GCB=90°,
即BG⊥DE.
∴BG=DE,BG⊥DE;
(2)BG与DE仍具有上述关系,即BG⊥DE,BG=DE
理由:如图(2),设BG与DC交于点M,与DE交于点H.
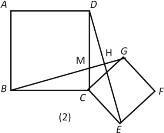
与(1)一样可证明△BCG≌△DCE,
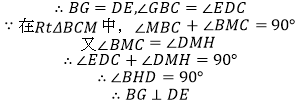
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是A,B,C,D三点,按如下步骤作图:①先分别以A,B两点为圆心,以大于
 AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于
AB的长为半径作弧,两弧相交于M、N两点,作直线MN;②再分别以B,C两点为圆心,以大于 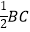 的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )
的长为半径作弧,两弧相交于G,H两点,作直线GH,GH与MN交于点P,若∠BAC=66°,则∠BPC等于( )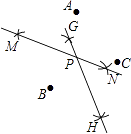
A.100°
B.120°
C.132°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图1,图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.

操作发现:小颖在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC的面积.
(1)在图1中,小颖所画的△ABC的三边长分别是AB=__________,BC=__________,AC=__________;△ABC的面积为__________.
解决问题:(2)已知△ABC中,AB=
 ,BC=2
,BC=2 ,AC=5
,AC=5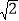 ,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=﹣x2+4x+c的图象经过A(1,y1),B(﹣1,y2),C(2+
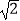 ,y3)三点,则y1、y2、y3的大小关系是( )
,y3)三点,则y1、y2、y3的大小关系是( )
A.y1<y2<y3
B.y1<y3<y2
C.y2<y3<y1
D.y2<y1<y3 -
科目: 来源: 题型:
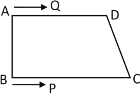
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2 cm/s的速度向点C运动,P,Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
(1)直接写出:QD=______cm,PC=_______cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=10cm,在直线AB上取一点C,使AC=16cm,则线段AB的中点与AC的中点的距离为( )
A.13cm或26cmB.6cm或13cmC.6cm或25cmD.3cm或13cm
-
科目: 来源: 题型:
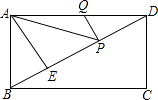
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为 .
相关试题

