【题目】如图,两条笔直的街道AB,CD相交于点O,街道OE,OF分别平分∠AOC,∠BOD,比较∠1与∠2的关系,并说明街道EOF是笔直的.

参考答案:
【答案】∠1=∠2, 街道EOF是笔直的,理由见解析
【解析】
根据对顶角相等可得∠AOC=∠BOD,再根据角平分线的定义可得∠1=![]() ∠AOC,∠2=
∠AOC,∠2=![]() ∠BOD,从而得到∠1=∠2,再根据AB是笔直的街道可得∠2+∠AOF=180°,求出∠1+∠AOF=180°,从而得解.
∠BOD,从而得到∠1=∠2,再根据AB是笔直的街道可得∠2+∠AOF=180°,求出∠1+∠AOF=180°,从而得解.
∵∠AOC和∠BOD是对顶角,
∴∠AOC=∠BOD,
∵OE,OF分别平分∠AOC,∠BOD,
∴∠1=![]() ∠AOC,∠2=
∠AOC,∠2=![]() ∠BOD,
∠BOD,
∴∠1=∠2,
∵AB是笔直的街道,
∴∠2+∠AOF=180°,
∴∠1+∠AOF=180°,
即∠EOF=180°,
∴EOF是一条直线,
即街道EOF是笔直的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O,OG是∠AOF的平分线,∠BOD=35°,∠COE=18°,则∠COG的度数是________.
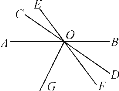
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O,∠BOD=45°,∠COF=80°.
(1)图中有多少对对顶角(不含平角)?
(2)每一对对顶角中,各角的度数是多少?
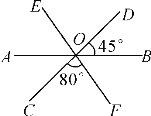
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b相交于点O,∠1=∠2.
(1)指出∠3的对顶角;
(2)指出∠5的补角;
(3)若∠1与∠4的度数之比为1∶4,求∠3的度数.
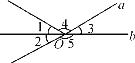
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形,寻找对顶角(不含平角).
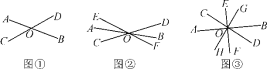
(1)如图①,图中共有______对对顶角;
(2)如图②,图中共有______对对顶角;
(3)如图③,图中共有______对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成__________对对顶角;
(5)若20条直线相交于一点,则可形成对顶角多少对?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

相关试题

