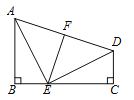
【题目】如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F.
(1)求证:F是AD中点;
(2)求∠AEF的度数.
参考答案:
【答案】(1)证明见解析;(2)45°
【解析】试题分析:(1)由题意,AB⊥BC,DC⊥BC,AB=EC,BE=CD,可证△ABE≌△ECD,可证AE=ED,且EF⊥AD,即可得证F是AD是中点.
(2)由(1)可推出,△AED为等腰直角三角形,所以∠AEF=45°.
试题解析:由题意,AB⊥BC,DC⊥BC,AB=EC,BE=CD,
所以△ABE≌△ECD,
所以AE=ED,
又EF⊥AD,
即可得证F是AD是中点;
(2)由(1)得,∠AEB+∠CED=90°;
所以∠AED=90°,
所以△AED为等腰直角三角形,
所以∠AEF=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4
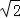 ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.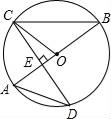
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,AB=5,射线AX垂直于AC,点A为垂足,一条长度为5的线段PQ的两个端点P、Q分别在边AC和射线AX上运动,则当AP=___________ 时,ΔABC与ΔPQA全等.

-
科目: 来源: 题型:
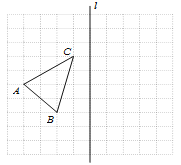
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
-
科目: 来源: 题型:
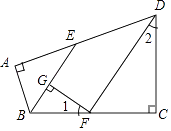
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与2互为相反数,则a+1的值为( )
A.﹣3.B.﹣1.C.1.D.3.
-
科目: 来源: 题型:
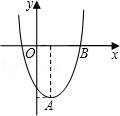
查看答案和解析>>【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
相关试题

