搜索
【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+2与y轴交于点A，点B是抛物线的顶点，点C与点A是抛物线上关于对称轴对称的两个点，点D在x轴上运动，则四边形ABCD的两条对角线的长度之和的最小值为_____．
参考答案：
【答案】
【解析】
先将函数化为顶点式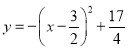
，所以顶点坐标
，对称轴为直线
，BD最小值为
，又点C与点A是抛物线上的两个对称点，对称轴为直线，所以C（3，2），AC＝3，因此四边形ABCD的两条对角线的长度之和AC+BD的最小值为
．
解：∵y＝﹣x2+3x+2＝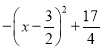
，
∴，对称轴为直线
∴当BD⊥x轴时，BD最小，BD＝
令x＝0，则y＝2，
∵C与点A是抛物线上关于对称轴对称的两个点，对称轴为直线，
∴C（3，2）
∴AC＝3，
四边形ABCD的两条对角线的长度之和AC+BD的最小值为
，
故答案为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=12，点D在边BC上，点E在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G，若EF=EG，则CD的长为（ ）
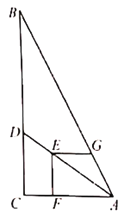
A.3.6B.4C.4.8D.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF．下列结论正确的是（ ）
A. CE=
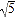B. EF=
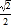C. cos∠CEP=
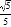D. HF2=EFCF -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C，D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为______.
-
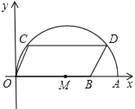
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC于D，下列条件：（1）∠B+∠DAC＝90°；（2）∠B＝∠DAC；（3）
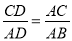；（4）AB2＝BDBC．其中一定能够判定△ABC是直角三角形的有（填序号）_____．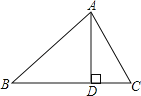
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在矩形ABCD中，AB<AD，对角线AC，BD相交于点O，动点P由点A出发，沿AB-BC→CD向点D运动设点P的运动路程为x，△AOP的面积为y，y与x的函数关系图象如图②所小示，则AD的长为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊙O中，半径OA与弦BD垂直，点C在⊙O上，∠AOB＝80°
(1) 若点C在优弧BD上，求∠ACD的大小
(2) 若点C在劣弧BD上，直接写出∠ACD的大小
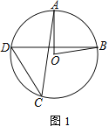
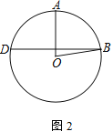
相关试题
