【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

参考答案:
【答案】(1)90°,直径所对的圆周角是直角;
(2)△EAD是等腰三角形,理由见解析;
(3)BD=![]()
【解析】试题分析:(1)根据AB是⊙O的直径,点C在⊙O上利用直径所对的圆周角是直角即可得到结论;
(2)根据∠ABC的平分线与AC相交于点D,得到∠CBD=∠ABE,再根据AE是⊙O的切线得到∠EAB=90°,从而得到∠CDB+∠CBD=90°,等量代换得到∠AED=∠EDA,从而判定△EAD是等腰三角形.
(3)证得△CDB∽△AEB后设BD=5x,则CB=4x,CD=3x,从而得到CA=CD+DA=3x+6,然后在直角三角形ACB中,利用AC2+BC2=AB2得到(3x+6)2+(4x)2=82解得x后即可求得BD的长.
试题解析:(1)∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角)
(2)△EAD是等腰三角形.
证明:∵∠ABC的平分线与AC相交于点D,
∴∠CBD=∠ABE
∵AE是⊙O的切线,∴∠EAB=90°
∴∠AEB+∠EBA=90°,
∵∠EDA=∠CDB,∠CDB+∠CBD=90°,
∵∠CBE=∠ABE,
∴∠AED=∠EDA,
∴AE=AD
∴△EAD是等腰三角形.
(3)解:∵AE=AD,AD=6,
∴AE=AD=6,
∵AB=8,
∴在直角三角形AEB中,EB=10
∵∠CDB=∠E,∠CBD=∠ABE
∴△CDB∽△AEB,
∴![]() ,
,
∴设CB=4x,CD=3x则BD=5x,
∴CA=CD+DA=3x+6,
在直角三角形ACB中,
AC2+BC2=AB2
即:(3x+6)2+(4x)2=82,
解得:x=﹣2(舍去)或x=![]()
∴BD=5x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,BC=4
 ,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,试求CM+MN的最小值.
,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,试求CM+MN的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据3,2,x,1,2的平均数是2,则这组数据的中位数和众数分别是( )
A.3,2
B.2,1
C.2,2.5
D.2,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣2,3)平面直角坐标系中先向左平移2个单位长度,再向上平移1个单位长度,得到的点的坐标是 .
-
科目: 来源: 题型:
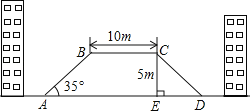
查看答案和解析>>【题目】如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,天桥高度CE=5m,求天桥下底AD的长度?(结果精确到0.1m,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(-2,-1)在第 _________ 象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-2,2)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

