【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.

(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
参考答案:
【答案】(1)证明见解析;(2)①5;②16.
【解析】试题分析:(1)根据∠OEF=90°得出∠OED+∠CEF=90°,根据∠CEF+∠CFE=90°得出∠OED=∠EFC,最后根据∠D=∠C即可证出△ODE∽△ECF;
(2)①根据△ODE∽△ECF,得出ODCF=DEEC,设DE=x,得出ODCF=-(x-4)2+16,从而求出最大值,设此时半径为r,根据OD2+DE2=OE2,得出(8-r)2+42=r2,解方程即可;
②在Rt△ODE中,根据OD2+DE2=OE2,OA=OE,得出(8-OE)2+x2=OE2,求出OE=4+![]() ,OD=4-
,OD=4-![]() ,根据Rt△DOE∽Rt△CEF,得出
,根据Rt△DOE∽Rt△CEF,得出![]() ,代入得出CF=
,代入得出CF=![]() ,EF=
,EF=![]() ,最后根据△CEF的周长=CE+CF+EF代入计算即可得出△CEF的周长=16,是定值.
,最后根据△CEF的周长=CE+CF+EF代入计算即可得出△CEF的周长=16,是定值.
试题解析:(1)证明:∵EF切⊙O于点M,
∴∠OEF=90°,
∴∠OED+∠CEF=90°,
∵∠C=90°,
∴∠CEF+∠CFE=90°,
∴∠OED=∠EFC,
∵∠D=∠C=90°,
∴△ODE∽△ECF;
(2)解:①由(1)知:△ODE∽△ECF,
∴![]() ,
,
∴ODCF=DEEC,
∵DE=x,
∴EC=8-x,
∴ODCF=x(8-x)=-x2+8x=-(x-4)2+16,
当x=4时,ODCF的值最大,最大值为16,
设此时半径为r,则OA=OE=r,OD=8-r,
在Rt△ODE中,
∵OD2+DE2=OE2,
∴(8-r)2+42=r2,
解得r=5,
即此时半径长为5;
②△CEF的周长为定值,△CEF的周长=16,
在Rt△ODE中,OD2+DE2=OE2,OA=OE,
即:(8-OE)2+x2=OE2,
∴OE=4+![]() ,OD=8-OE=4-
,OD=8-OE=4-![]() ,
,
∵Rt△DOE∽Rt△CEF,
即![]() ,
,
∴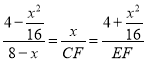 ,
,
解得:CF=![]() ,EF=
,EF=![]() ,
,
∴△CEF的周长=CE+CF+EF=8-x+![]() +
+![]() =16.
=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是正整数,若有序数对(a,b)使得
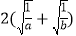 的值也是整数,则称(a,b)是
的值也是整数,则称(a,b)是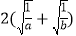 的一个“理想数对”,如(1,4)使得
的一个“理想数对”,如(1,4)使得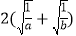 =3,所以(1,4)是
=3,所以(1,4)是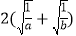 的一个“理想数对”.请写出
的一个“理想数对”.请写出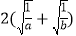 其他所有的“理想数对”: __________.
其他所有的“理想数对”: __________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
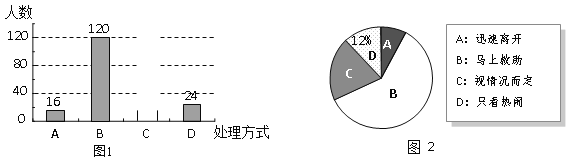
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二元一次方程y﹣x=1,若y的值大于﹣1,则x的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】尽管受到国际金融危机的影响,但义乌市经济依然保持了平稳增长.据统计,截止到今年4月底,该市金融机构存款余额约为1193亿元,用科学记数法应记为元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在本学期某次考试中,某校初二(1)、初二(2)两班学生数学成绩统计如下表:
分数
50
60
70
80
90
100
人
数
二(1)班
3
5
16
3
11
12
二(2)班
2
5
11
12
13
7
请根据表格提供的信息回答下列问题:
(1)二(1)班平均成绩为______分,二(2)班平均成绩为______分,从平均成绩看两个班成绩谁优谁次?
(2)二(1)班众数为______分,二(2)班众数为______分.从众数看两个班的成绩谁优谁次?______.
(3)已知二(1)班的方差大于二(2)班的方差,那么说明什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形
B.线段
C.矩形
D.平行四边形
相关试题

