【题目】丰富的图形世界里有奇妙的数量关系,让我们通过下面这些几何体开始神奇的探索之旅.
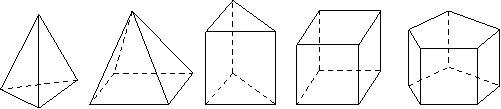
观察:下面这些几何体都是简单几何体,请您仔细观察.
![]()
统计:每个几何体都会有棱(棱数为E)、面(面数为F)、顶点(顶点数为V),现将有关数据统计,完成下表.
几何体 | a | b | c | d | e |
棱数(E) | 6 | 9 | 15 | ||
面数(F) | 4 | 5 | 5 | 6 | |
顶点数(V) | 4 | 5 | 8 |
发现:(1)简单几何中,![]() ;
;
(2)简单几何中,每条棱都是 个面的公共边;
(3)在正方体中,每个顶点处有 条棱,每条棱都有 个顶点,所以有2![]() 3
3![]() .
.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有 条棱, 个顶点,每个顶点处有 条棱.
参考答案:
【答案】统计:
几何体 | a | b | c | d | e |
棱数(E) | 6 | 8 | 9 | 12 | 15 |
面数(F) | 4 | 5 | 5 | 6 | 7 |
顶点数(V) | 4 | 5 | 6 | 8 | 10 |
发现:(1)2 ;(2)2;(3)3,2
应用:30,20,3.
【解析】
试题统计:仔细分析所给图形的特征即可得到结果;
发现:根据表格中的数据依次分析即可得到结果;
应用:应用所发现的规律即可得到结果.
统计:
几何体 | a | b | c | d | e |
棱数(E) | 6 | 8 | 9 | 12 | 15 |
面数(F) | 4 | 5 | 5 | 6 | 7 |
顶点数(V) | 4 | 5 | 6 | 8 | 10 |
发现:(1)简单几何中,![]() 2;
2;
(2)简单几何中,每条棱都是2个面的公共边;
(3)在正方体中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2![]() 3
3![]() .
.
应用:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.请问它有30条棱,20个顶点,每个顶点处有3条棱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次设计比赛中,小军10次射击的成绩是:6环1次,7环3次,8环2次,9环3次,10环1次,关于他的射击成绩,下列说法正确的是( )
A.极差是2环
B.中位数是8环
C.众数是9环
D.平均数是9环 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是_______cm3.

-
科目: 来源: 题型:
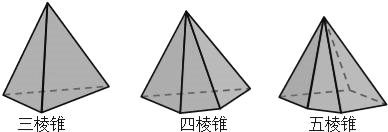
查看答案和解析>>【题目】设棱锥的顶点数为V,面数为F,棱数为E.
(1)观察与发现:三棱锥中,V3= ,F3= ,E3= ;
五棱锥中,V5= ,F5= ,E5= ;
(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;
②n棱锥中,Vn= ,Fn= ,En= ;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系: ;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E= ;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.
-
科目: 来源: 题型:
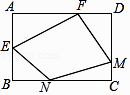
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )
A.2+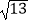
B.2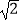 +2
+2 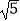
C.5+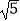
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

相关试题

