搜索
【题目】某长途汽车客运公司规定：旅客可免费带一定重量的行李，如果超过规定重量需要购买行李票，设旅客最多可免费携带30千克的行李，超过30千克后每增加1千克，需购买0.5元的行李票，求行李票y(元)与行李重量x(千克)(x＞30)之间的函数关系式，如果某旅客买了12元的行李票，那么他带的行李重多少千克？
参考答案：
【答案】y=0.5(x-30)；54千克.
【解析】
根据题意，当行李重量为x时，超过(x-30)千克，所以可以列出y与x的函数关系式.
根据题意可得y=0.5(x-30)；
当y=12，则0.5(x-30)=12，
解得x=54，
所以他带的行李重54千克.
故答案为：y=0.5(x-30)；54千克.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一台电视机的原价是a元，现按原价的9折出售，则这台电视机现在的售价为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种储蓄的月利率是0.36%,今存入本金100元,求本息和(本金与利息的和)y(元)与所存月数x之间的函数关系式，并计算5个月后的本息和
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图 1，二次函数
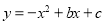的图像过点 A （3，0），B （0，4）两点，动点 P 从 A 出发，在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动，过点P作 PD⊥y 于点 D ，交抛物线于点 C ．设运动时间为 t （秒）．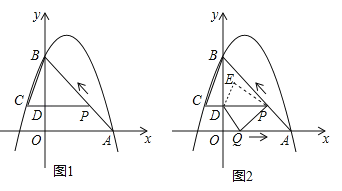
（1）求二次函数
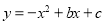的表达式；（2）连接 BC ，当t＝
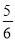时，求△BCP的面积；（3）如图 2，动点 P 从 A 出发时，动点 Q 同时从 O 出发，在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动，当点 P 与 B 重合时，P 、 Q 两点同时停止运动，连接 DQ 、 PQ ，将△DPQ沿直线 PC 折叠到 △DPE ．在运动过程中，设 △DPE 和 △OAB重合部分的面积为 S ，直接写出 S 与 t 的函数关系式及 t 的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线OC，BC的函数关系式分别是y1=
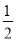x和y2=-x+6，两直线的交点为C.（1）求点C的坐标，并直接写出y1＞y2时x的范围；
（2）在直线y1上找点D，使△DCB的面积是△COB的一半，求点D的坐标；
（3）点M（t,0）是
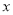轴上的任意一点，过点M作直线l⊥
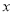轴，分别交直线y1、 y2于点E、F，当E、F两点间的距离不超过4时，求t的取值范围．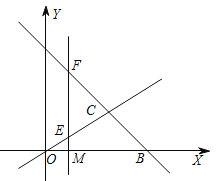
相关试题
