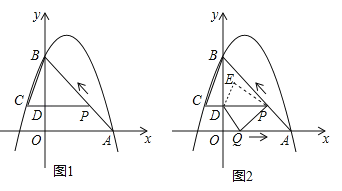
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
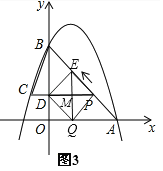
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
参考答案:
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3)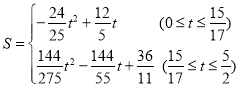 .
.
【解析】
试题分析:(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)如图1,要想求△BCP的面积,必须求对应的底和高,即PC和BD;先求OD,再求BD,PC是利用点P和点C的横坐标求出,要注意符号;
(3)分两种情况讨论:①△DPE完全在△OAB中时,即当![]() 时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当
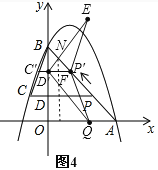
时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当![]() 时,如图4所示,△PDN就是重合部分的面积S.
时,如图4所示,△PDN就是重合部分的面积S.
试题解析:(1)把A(3,0),B(0,4)代入![]() 中得:
中得:
![]() ,解得:
,解得:![]() ,∴解析式为:
,∴解析式为:![]() ;
;
(2)如图1,当![]() 时,AP=2t,∵PC∥x轴,∴
时,AP=2t,∵PC∥x轴,∴![]() ,∴
,∴![]() ,∴OD=
,∴OD=![]() =
=![]() =
=![]() ,当y=
,当y=![]() 时,
时,![]() =
=![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,∴C(﹣1,
,∴C(﹣1,![]() ),由
),由![]() ,得
,得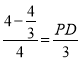 ,则PD=2,∴S△BCP=
,则PD=2,∴S△BCP=![]() ×PC×BD=
×PC×BD=![]() =4;
=4;
(3)分两种情况讨论:①如图3,当点E在AB上时,由(2)得OD=QM=ME=![]() ,∴EQ=
,∴EQ=![]() ,由折叠得:EQ⊥PD,则EQ∥y轴,∴
,由折叠得:EQ⊥PD,则EQ∥y轴,∴![]() ,∴
,∴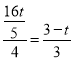 ,∴t=
,∴t=![]() ,同理得:PD=
,同理得:PD=![]() ,∴当
,∴当![]() 时,S=S△PDQ=
时,S=S△PDQ=![]() ×PD×MQ=
×PD×MQ=![]() ,
,![]() ;
;
②当![]() 时,如图4,P′D′=
时,如图4,P′D′=![]() ,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,
,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,![]() ),∵AB的解析式为:
),∵AB的解析式为:![]() ,D′E的解析式为:
,D′E的解析式为:![]() ,则交点N(
,则交点N(![]() ,
,![]() ),∴S=S△P′D′N=
),∴S=S△P′D′N=![]() ×P′D′×FN=
×P′D′×FN=![]() ,∴
,∴![]() .
.
综上所述: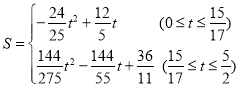 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一台电视机的原价是a元,现按原价的9折出售,则这台电视机现在的售价为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种储蓄的月利率是0.36%,今存入本金100元,求本息和(本金与利息的和)y(元)与所存月数x之间的函数关系式,并计算5个月后的本息和
-
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车客运公司规定:旅客可免费带一定重量的行李,如果超过规定重量需要购买行李票,设旅客最多可免费携带30千克的行李,超过30千克后每增加1千克,需购买0.5元的行李票,求行李票y(元)与行李重量x(千克)(x>30)之间的函数关系式,如果某旅客买了12元的行李票,那么他带的行李重多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OC,BC的函数关系式分别是y1=
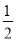 x和y2=-x+6,两直线的交点为C.
x和y2=-x+6,两直线的交点为C.(1)求点C的坐标,并直接写出y1>y2时x的范围;
(2)在直线y1上找点D,使△DCB的面积是△COB的一半,求点D的坐标;
(3)点M(t,0)是
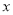 轴上的任意一点,过点M作直线l⊥
轴上的任意一点,过点M作直线l⊥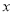 轴,分别交直线y1、 y2于点E、F,当E、F两点间的距离不超过4时,求t的取值范围.
轴,分别交直线y1、 y2于点E、F,当E、F两点间的距离不超过4时,求t的取值范围.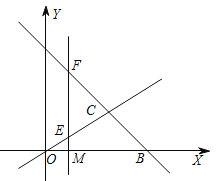
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

相关试题

