【题目】在等腰△ABC中,AB=AC,则有BC边上的中线,高线和∠BAC的平分线重合于AD(如图一).若将等腰△ABC的顶点A向右平行移动后,得到△A′BC(如图二),那么,此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 , , .(填A′D、A′E、A′F)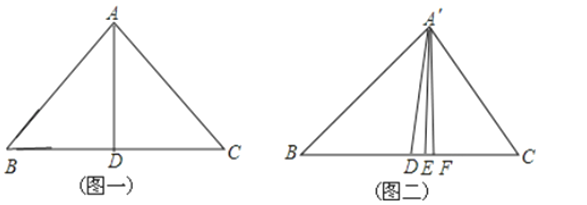
参考答案:
【答案】A′D;AF;AE
【解析】解:
在等腰△ABC中,AB=AC,则有BC边上的中线,高线和∠BAC的平分线重合于AD(如图一).若将等腰△ABC的顶点A向右平行移动后,得到△A′BC(如图二),那么,此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 A′D,AF,AE,
所以答案是:A′D,A′F,A′E.
【考点精析】掌握平移的性质是解答本题的根本,需要知道①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理说明:
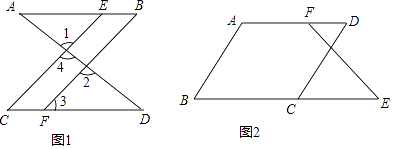
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下: 因为∠1=∠2(已知),且∠1=∠4()
所以∠2=∠4(等量代换)
所以CE∥BF()
所以∠=∠3()
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD()
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE. 证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD ()
∴∠B=()
又∵∠B=∠D(已知),
∴∠=∠(等量代换)
∴AD∥BE()
∴∠E=∠DFE() -
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值等于其相反数的数一定是( )
A.负数
B.正数
C.负数或零
D.正数或零 -
科目: 来源: 题型:
查看答案和解析>>【题目】若直角三角形中的两个锐角之差为16°,则较大的一个锐角的度数是( )
A.37°
B.53°
C.26°
D.63° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长l与边长a的关系
C.矩形的长为a , 宽为20,其面积S与a的关系
D.矩形的面积为40,长a与宽b之间的关系 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式相乘的结果是a2-a-6的是( )
A.(a-2)(a+3) B.(a+2)(a-3) C.(a-6)(a+1) D.(a+6)(a-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x是实数,y=|x-1|+|x+1|,下列结论正确的是( ).
A.y没有最小值
B.只有一个x使y取到最小值
C.有有限多个x(不止一个)使y取到最小值
D.有无穷多个x使y取到最小值
相关试题

