【题目】小明学完了统计知识后,从“中国环境保护网”上查询到他所居住城市2009年全年的空气质量级别资料,用简单随机抽样的方法选取30天,并列出下表:
空气质量级别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | a | 15 | 2 | 1 | 0 |
请你根据以上信息解答下面问题:
(1)这次抽样中“空气质量不低于良”的频率为多少?
(2)根据这次抽样的结果,请你估计2009年全年(共365天)空气质量为优的天数是多少?
参考答案:
【答案】(1)0.9(2)146天
【解析】试题分析:(1)、根据总天数减去轻度污染、中度污染和重度污染的天数得出优和良的总天数,从而得出概率;(2)、首先根据总天数求出空气质量为优的天数,从而求出全年的天数.
试题解析:(1)∵这次抽样中,“空气质量不低于良”的频数是30﹣0﹣1﹣2=27,
∴频率为![]() =0.9;
=0.9;
(2)∵a=30﹣(15+2+1)=12,
∴365×![]() =146.
=146.
答:2009年全年(共365天)空气质量为优的天数大约为146天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+m+2=0有两个不等的实数根x1和x2
(1)求m的取值范围并证明x1x2=m+2;
(2)若|x1﹣x2|=2,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
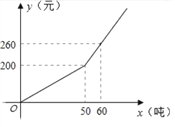
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收
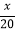 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量. -
科目: 来源: 题型:
查看答案和解析>>【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣
 , x1x2=
, x1x2=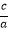 , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣ =﹣
=﹣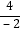 =2,x1x2=
=2,x1x2=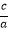 =
=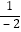 =﹣
=﹣
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣ )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1 , x2 , 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
2
5
6
4
10
3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3a2=a6 B. (﹣a2)3=a6 C. a3+a4=a7 D. a2(a3)4=a14
相关试题

