【题目】已知关于x的一元二次方程x2﹣2x+m+2=0有两个不等的实数根x1和x2
(1)求m的取值范围并证明x1x2=m+2;
(2)若|x1﹣x2|=2,求m的值.
参考答案:
【答案】解:(1)∵关于x的一元二次方程x2﹣2x+m+2=0有两个不等的实数根x1和x2 ,
所以△=(﹣2)2﹣4(m+2)=﹣4m﹣4>0
解得m<﹣1,
根据求根公式![]() ,
,![]()
∴![]() ;
;
(2)根据根与系数的关系得x1+x2=2,x1x2=m+2,
∵|x1﹣x2|=2,
∴(x1﹣x2)2=4,
∴(x1+x2)2﹣4x1x2=4,
∴4﹣4(m+2)=4,
解得m=﹣2.
【解析】(1)根据判别式的意义得到△=(﹣2)2﹣4(m+2)=﹣4m﹣4>0解得m<﹣1,再利用求根公式解方程,然后计算x1x2;
(2)先根据根与系数的关系得x1+x2=2,x1x2=m+2,再把|x1﹣x2|=2两边平方得到(x1﹣x2)2=4,接着利用完全平方公式变形得到(x1+x2)2﹣4x1x2=4,所以4﹣4(m+2)=4,
然后解关于m的方程即可.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0有两个实数根x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知a、b是方程x2+15x+5=0的二根,则 =?
=?
(2)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
(3)结合二元一次方程组的相关知识,解决问题:已知 和
和 是关于x,y的方程组
是关于x,y的方程组 的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣
的两个不相等的实数解.问:是否存在实数k,使得y1y2﹣ =2?若存在,求出的k值,若不存在,请说明理由.
=2?若存在,求出的k值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】笔尖在纸上写字说明;车轮旋转时看起来象个圆面,这说明;一枚硬币在光滑的桌面上快速旋转形成一个球,这说明 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
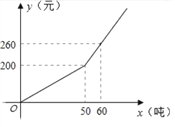
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收
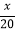 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明学完了统计知识后,从“中国环境保护网”上查询到他所居住城市2009年全年的空气质量级别资料,用简单随机抽样的方法选取30天,并列出下表:
空气质量级别
优
良
轻度污染
中度污染
重度污染
天数
a
15
2
1
0
请你根据以上信息解答下面问题:
(1)这次抽样中“空气质量不低于良”的频率为多少?
(2)根据这次抽样的结果,请你估计2009年全年(共365天)空气质量为优的天数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣
 , x1x2=
, x1x2=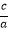 , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣ =﹣
=﹣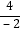 =2,x1x2=
=2,x1x2=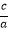 =
=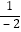 =﹣
=﹣
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣ )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1 , x2 , 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
相关试题

