【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的x的取值范围.

参考答案:
【答案】(1)y=![]() ;y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5;
;y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5;
【解析】
(1)把A(﹣2,﹣5)代入y=![]() 求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式即可;(2)先求得OB的长,再根据S△AOC=S△AOB+S△BOC即可求得△AOC的面积;(3)根据图象和交点坐标即可求得.
求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式即可;(2)先求得OB的长,再根据S△AOC=S△AOB+S△BOC即可求得△AOC的面积;(3)根据图象和交点坐标即可求得.
(1)把点A(﹣2,﹣5)代入反比例函数的解析式y=![]() 得:﹣5=
得:﹣5=![]() ,
,
解得:m=10,
即反比例函数的解析式为:y=![]() ,
,
把点C(5,n)代入解析式y=![]() 得:n=2,
得:n=2,
即点C的坐标为(5,2),
把点A(﹣2,﹣5)和点C(5,2)代入y=kx+b得:
![]() ,
,
解得:![]() ,
,
即一次函数的表达式为y=x﹣3,
(2)把x=0代入y=x﹣3得:y=﹣3,
即OB=3,
∵C(5,2),A﹙-2,-5﹚,
∴S△AOC=S△AOB+S△BOC=![]() OB|2|+
OB|2|+![]() OB5=
OB5=![]() OB(2+5)=10.5.
OB(2+5)=10.5.
(3)通过观察图象可知:
使一次函数的值大于反比例函数的x的取值范围为:﹣2<x<0或x>5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
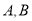 是数轴上的两点,
是数轴上的两点,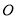 为原点,点
为原点,点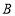 表示的数是1,点
表示的数是1,点 在点
在点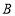 的左侧,
的左侧, .
.
(1)求点
 表示的数;
表示的数;(2)数轴上的一点
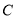 在点
在点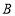 的右侧,设点
的右侧,设点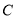 表示的数是
表示的数是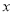 ,若点
,若点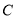 到
到 ,
,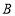 两点的距离的和是15,求
两点的距离的和是15,求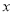 的值;
的值;(3)动点
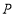 从
从 点出发,以每秒2个单位的速度向右运动,同时动点
点出发,以每秒2个单位的速度向右运动,同时动点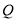 从
从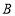 点出发,以每秒1个单位的速度向右运动,设运动时间为
点出发,以每秒1个单位的速度向右运动,设运动时间为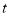 秒,是否存在这样的
秒,是否存在这样的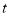 值,使
值,使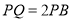 ,若存在,请求出
,若存在,请求出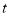 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司提供的移动通讯服务的收费标准有两种套餐如表
 套餐
套餐 套餐
套餐每月基本服务费(元)
20
30
每月免费通话时间(分)
100
150
每月超过免费通话时间加收通话费(元/分)
0.4
0.5
李民选用了
 套餐
套餐(1)5月份李民的通话时间为120分钟,这个月李民应付话费多少元?
(2)李民6月份的通话时间超过了150分钟,根据自己6月份的通话时间情况计算,如果自己选用
 套餐可以省4元钱,李民6月份的通话时间是多少分钟?
套餐可以省4元钱,李民6月份的通话时间是多少分钟?(3)10月份李民改用了
 套餐,李民发现如果与9月份交相同的话费,10月份他可以多通话15分钟,李民9月份交了多少话费?
套餐,李民发现如果与9月份交相同的话费,10月份他可以多通话15分钟,李民9月份交了多少话费? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )

A.△ABC中,AB边上的高是CEB.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CED.△ACD中,CD边上的高是AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】从徐州到某地,若乘坐普通列车,行程为520km;若乘坐高铁,行程为400km.已知高铁的平均速度是普通列车的2.5倍,从徐州到该市乘坐高铁比乘坐普通列车少用3h.求高铁行驶的平均速度.
相关试题

