【题目】如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 . 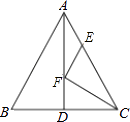
参考答案:
【答案】![]()
【解析】解:作BE⊥AC垂足为E,交AD于F,此时CF+EF最小.

理由如下:∵AB=AC,AD是中线,
∴AD⊥BC,
∴FB=FC,
∴CF+EF=BF+EF,
∵线段BE是垂线段,根据垂线段最短,
∴点E、点F、就是所找的点.
∵ ![]() BCAD=
BCAD= ![]() ACBE,
ACBE,
∴ ![]() ×20×24=
×20×24= ![]() ×26×BE,
×26×BE,
∴BE= ![]() ,
,
∴CF+EF的最小值=BE= ![]() ,
,
故答案为 ![]() .
.
根据等腰三角形的三线合一,得到AD⊥BC,FB=FC,CF+EF=BF+EF,由线段BE是垂线段,根据垂线段最短,得到点E、点F、就是所找的点,求出CF+EF的最小值=BE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲 , y乙与x之间的函数图象如图所示,结合图象解答下列问题:
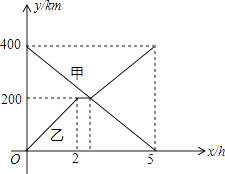
(1)求:y甲与x的函数关系式,并写出自变量x的取值范围;
(2)乙车休息了h;
(3)当两车相距80km时,直接写出x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC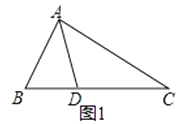
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…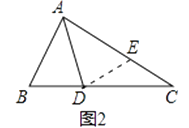
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.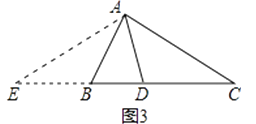
(2)【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.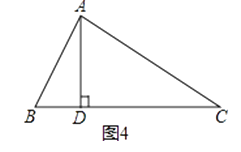
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠B的度数是( )
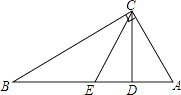
A.60°
B.45°
C.30°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】一滴水的质量约0.000053 kg,用科学记数法表示这个数为_____kg.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步了解八年级500名学生的身体素质情况,体育老师对八年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图如下所示:


请结合图表完成下列问题:
(1)表中的m= , 次数在140≤x<160这组的频率为;
(2)请你把频数分布直方图补充完整;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,求八年级合格的学生有多少人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,交BF于C.
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.

相关试题

