Question

【题目】如图，AB是半圆的直径，O为圆心，AD、BD是半圆的弦，且∠PDA=∠PBD．

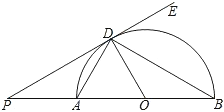
（1）判断直线PD是否为⊙O的切线，并说明理由；

（2）如果∠BDE=60°，PD=，求PA的长．

Answer 1

【答案】（1）PD是⊙O的切线．（2）1．

【解析】

试题分析：（1）要证是直线PD是为⊙O的切线，需证∠PDO=90°．因为AB为直径，所以∠ADO+∠ODB=90°，由∠PDA=∠PBD=∠ODB可得∠ODA+∠PDA=90°，即∠PDO=90°．

（2）根据已知可证△AOD为等边三角形，∠P=30°．在Rt△POD中运用三角函数可求解．

解：（1）PD是⊙O的切线．理由如下：

∵AB为直径，

∵∠ADB=90°，

∴∠ADO+∠ODB=90°．

∵∠PDA=∠PBD=∠ODB，

∴∠ODA+∠PDA=90°．即∠PDO=90°．

∴PD是⊙O的切线．

（2）∵∠BDE=60°，∠ADB=90°，

∴∠PDA=180°﹣90°﹣60°=30°，

又PD为半圆的切线，所以∠PDO=90°，

∴∠ADO=60°，又OA=OD，

∴△ADO为等边三角形，∠AOD=60°．

在Rt△POD中，PD=，

∴OD=1，OP=2，

PA=PO﹣OA=2﹣1=1．