【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
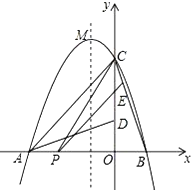
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
参考答案:
【答案】(1)y=﹣x2﹣2x+3(2)![]() (3)Q(
(3)Q(![]() ,
,![]() ),或(
),或(![]() ,
,![]() )
)
【解析】试题分析:(1)根据题意求出A、B、C的坐标,然后根据待定系数法求函数的解析式即可;
(2)设点P(x,0),则PB=1﹣x,根据三角形的面积可得二次函数的解析式,然后根据二次函数的最值可求解;
(3)根据配方法求出顶点的坐标,然后根据等腰三角形的性质,结合勾股定理列方程可求解.
试题解析:(1)∵B(1,0),C(0,3),∴OB=1,OC=3.
∵△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
∴OA=OC=3,∴A(﹣3,0),
∵点A,B,C在抛物线上,
∴ ,∴
,∴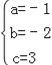 ,∴二次函数的解析式为y=﹣x2﹣2x+3,
,∴二次函数的解析式为y=﹣x2﹣2x+3,
(2)设点P(x,0),则PB=1﹣x,
∴S△PBE=![]() (1﹣x)2,
(1﹣x)2,
∴S△PCE=S△PBC﹣S△PBE=![]() PB×OC﹣
PB×OC﹣![]() (1﹣x)2=
(1﹣x)2=![]() (1﹣x)×3﹣
(1﹣x)×3﹣![]() (1﹣x)2=﹣
(1﹣x)2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
当x=1时,S△PCE的最大值为![]() .
.
(3)∵二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点坐标(﹣1,4),
∵△OMQ为等腰三角形,OM为底,
∴MQ=OQ,
∴![]() =
=![]() ,
,
∴8x2+18x=7=0,∴x=![]() ,∴y=
,∴y=![]() 或y=
或y=![]() ,
,
∴Q(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】第十七届西洽会上,延安新区签约4个项目,总投资额11 536 000 000元,则11 536 000 000用科学记数法可表示为( )
A.115.36×108
B.1.1536×109
C.1.1536×1010
D.11.56×109 -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是________(写成两数平方差的形式);

(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是________,长是________,面积是________(写成多项式乘法的形式);
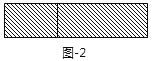
(3)比较左、右两图的阴影部分面积,可以得到乘法公式________(用式子表达).
-
科目: 来源: 题型:
查看答案和解析>>【题目】园林部门用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个,挂放在迎宾大道两侧,搭配每个造型所要花盆数如表,综合上述信息,解答下列问题.
造型
甲
乙
A
90盆
30盆
B
40盆
100盆
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1200元,选(1)中那种方案的成本最低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题:先化简,再求值
(1)先化简,再求值:x 2 -(x+2)(2-x)-2(x-5) 2 , 其中x=3.
(2)解不等式组
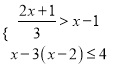 ,并求它的整数解.
,并求它的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
A.289(1﹣x)2=256
B.256(1﹣x)2=289
C.289(1﹣2x)=256
D.256(1﹣2x)=289 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由4个全等的正方形组成的L形图案,请按下列要求画图:
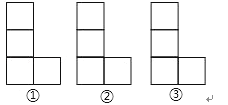
(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图案②中添画1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图案中改变1个正方形的位置,画成图案③,使它既成中心对称图形,又成轴对称图形.
相关试题

