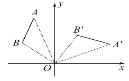
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-1,3)的对应点A′的坐标是________.
参考答案:
【答案】(3,1)
【解析】
由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′,∠AOA′=90°,作AC⊥y轴于C,A′C′⊥x轴于C′,就可以得出△ACO≌△A′C′O,就可以得出AC=A′C′,CO=C′O,由A的坐标就可以求出结论.
∵线段AB绕点O顺时针旋转90°得到线段A′B′,
∴△ABO≌△A′B′O′,∠AOA′=90°,
∴AO=A′O.
作AC⊥y轴于C,A′C′⊥x轴于C′,
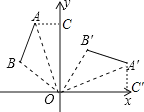
∴∠ACO=∠A′C′O=90°.
∵∠COC′=90°,
∴∠AOA′-∠COA′=∠COC′-∠COA′,
∴∠AOC=∠A′OC′.
在△ACO和△A′C′O中,
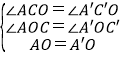 ,
,
∴△ACO≌△A′C′O(AAS),
∴AC=A′C′,CO=C′O.
∵A(-1,3),
∴AC=1,CO=3,
∴A′C′=1,OC′=3,
∴A′(3,1).
故答案为(3,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=
 ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.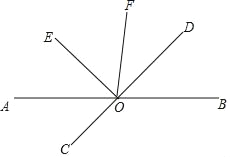
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,我市组织了一次初三年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分)
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
人数
1
2
3
3
6
7
5
8
15
9
11
12
8
6
4
成绩分组
频数
频率
35≤x<38
3
0.03
38≤x<41
a
0.12
41≤x<44
20
0.20
44≤x<47
35
0.35
47≤x≤50
30
b
请根据所提供的信息解答下列问题:
(1)样本的中位数是分;
(2)频率统计表中a= , b=;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?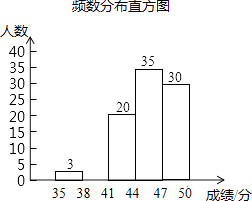
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
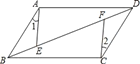
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=30°,∠B=60°,AB⊥AC。
(1)计算:∠DAB+∠B
(2)AB与CD平行吗?AD与BC平行吗?
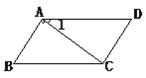
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
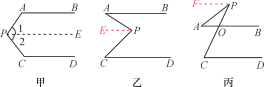
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.

A. 5050π B. 5050π+101 C. 5055π D. 5055π+101
相关试题

