搜索
【题目】如图，在平面直角坐标系中，正方形ABCD的顶点A、C分别在y轴、x轴上，以AB为弦的⊙M与x轴相切．若点A的坐标为（0，8），则圆心M的坐标为 （ ）
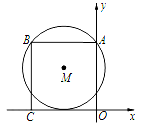
A．（-4，5） B．（-5，4） C．（-4，6） D．（-5，6）
参考答案：
【答案】A
【解析】
试题分析：过点M作
于D，连接AM，设
的半径为R，因为四边形OABC为正方形，定点A，C在坐标轴上，以边AB为弦的
与x轴相切，若点A的坐标为（0，8），所以
，
，AM=R，又因为
是直角三角形，利用勾股定理即可得到关于R的方程，解之即可．
过点M作于D，连接AM，设的半径为R，
∵以边AB为弦的与x轴相切，
，
∴
，
∴DE是直径的一部分；
∵四边形OABC为正方形，定点A，C在坐标轴上，点A的坐标为（0，8），
∴OA=AB=CB=OC=8，DM=8-R；
∴AD=BD=4（垂径定理）；
在
中
根据勾股定理可得
，
∴
∴R=5
∴M（-4，5）．
故选：A
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.射线AB与射线BA表示同一条射线
B.连接两点的线段叫做这两点的距离
C.平角是一条直线
D.若∠1+∠2=90°，∠1+∠3=90°，则∠2=∠3 -
科目： 来源： 题型：
查看答案和解析>>【题目】绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨，桃子12吨．现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售，已知一辆甲种货车可装枇杷4吨和桃子1吨，一辆乙种货车可装枇杷和桃子各2吨．
（1）王灿如何安排甲、乙两种货车可一次性地运到销售地有几种方案？
（2）若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王灿应选择哪种方案，使运输费最少？最少运费是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A（﹣4，﹣1），B（﹣5，﹣4），C（﹣1，﹣3），△ABC经过平移得到的△A′B′C′，△ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+6，y1+4）．
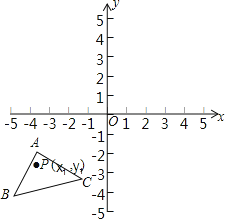
（1）请在图中作出△A′B′C′；
（2）写出点A′、B′、C′的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】矩形纸片ABCD中，AB=5，AD=4．
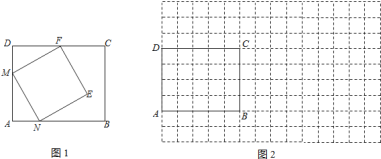
（1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是 ；（不必说明理由）
（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
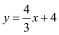分别交
轴，
轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．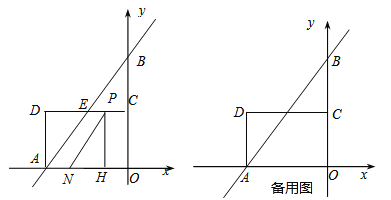
（1）直接写出点A，B的坐标，并求直线AB与CD交点E的坐标；
（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点N从点A出发，沿线段AO以每秒1个单位长度的速度向终点O运动，过点P作
，垂足为H，连接NP．设点P的运动时间为
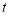秒．①若△NPH的面积为1，求
的值；②点Q是点B关于点A的对称点，问
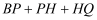是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠α=53°27′，则它的余角等于 ．
相关试题
