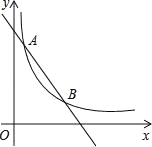
【题目】如图,一次函数y=-x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
参考答案:
【答案】(1)y=![]() ,点B的坐标为(3,1).(2)点P的坐标为(
,点B的坐标为(3,1).(2)点P的坐标为(![]() ,0).
,0).![]() .
.
【解析】
试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=![]() ,
,
得:3=k,
∴反比例函数的表达式y=![]() ,
,
联立两个函数关系式成方程组得: ,
,
解得:![]() ,或
,或![]() ,
,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
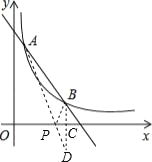
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得:![]() ,
,
解得:![]() ,
,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(3-1)-
×[1-(-1)]×(3-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列语句中:①实数不是有理数就是无理数;②无限小数都是无理数;③无理数都是无限小数;④根号的数都是无理数;⑤两个无理数之和一定是无理数;⑥所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数.正确的是_______(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形在平面直角坐标系中三个顶点的坐标为(-2,-3),(-2,1),(2,1),则第四个顶点的坐标为_________.
-
科目: 来源: 题型:
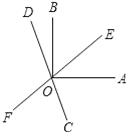
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种药品经过两次降价,药价从原来每盒60元降至到现在48.6元,则平均每次降价的百分比率是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
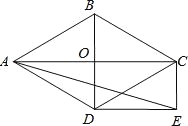
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2
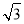 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子里有5只红球,3只白球,每只球除颜色以外都相同,从中任意摸出1只球,是红球的可能性(选填“大于”“小于”或“等于”)是白球的可能性.
相关试题

