【题目】 抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
⑴求直线![]() 的解析式;
的解析式;
⑵抛物线的对称轴上存在点![]() ,使
,使![]() ,利用图
,利用图![]() 求点
求点![]() 的坐标;
的坐标;
⑶点![]() 在
在![]() 轴右侧的抛物线上,利用图
轴右侧的抛物线上,利用图![]() 比较
比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
参考答案:
【答案】(1)y=﹣x+3;(2)(1,2+2![]() )或(1,﹣2﹣2
)或(1,﹣2﹣2![]() ),(3)当Q点横坐标为5时,∠OCA=∠OCQ;当Q点横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ..
),(3)当Q点横坐标为5时,∠OCA=∠OCQ;当Q点横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;当Q点横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ..
【解析】
试题分析:.(1)由抛物线解析式可求得B、C的坐标,利用待定系数法可求得直线BC的解析式;
(2)由直线BC解析式可知∠APB=∠ABC=45°,设抛物线对称轴交直线BC于点D,交x轴于点E,结合二次函数的对称性可求得PD=BD,在Rt△BDE中可求得BD,则可求得PE的长,可求得P点坐标;
(3)设Q(x,﹣x2+2x+3),当∠OCQ=∠OCA时,利用两角的正切值相等可得到关于x的方程,可求得Q点的横坐标,再结合图形可比较两角的大小.
试题解析:(1)在y=﹣x2+2x+3中,令y=0可得0=﹣x2+2x+3,解得x=﹣1或x=3,令x=0可得y=3,
∴B(3,0),C(0,3),∴可设直线BC的解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,∴直线BC解析式为y=﹣x+3;
(2)∵OB=OC,∴∠ABC=45°,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线对称轴为x=1,
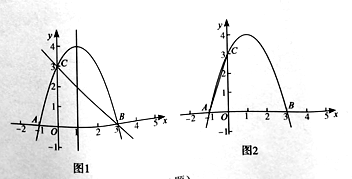
设抛物线对称轴交直线BC于点D,交x轴于点E,当点P在x轴上方时,如图1,

∵∠APB=∠ABC=45°,且PA=PB,
∴∠PBA=![]() ,∠DPB=
,∠DPB=![]() ∠APB=22.5°,
∠APB=22.5°,
∴∠PBD=67.5°﹣45°=22.5°,∴∠DPB=∠DBP,∴DP=DB,
在Rt△BDE中,BE=DE=2,由勾股定理可求得BD=2![]() ,
,
∴PE=2+2![]() ,∴P(1,2+2
,∴P(1,2+2![]() );
);
当点P在x轴下方时,由对称性可知P点坐标为(1,﹣2﹣2![]() );
);
综上可知P点坐标为(1,2+2![]() )或(1,﹣2﹣2
)或(1,﹣2﹣2![]() );
);
(3)设Q(x,﹣x2+2x+3),当点Q在x轴下方时,如图2,过Q作QF⊥y轴于点F,

当∠OCA=∠OCQ时,则△QEC∽△AOC,
∴![]() ,即
,即![]() ,解得x=0(舍去)或x=5,
,解得x=0(舍去)或x=5,
∴当Q点横坐标为5时,∠OCA=∠OCQ;
当Q点横坐标大于5时,则∠OCQ逐渐变小,故∠OCA>∠OCQ;
当Q点横坐标小于5且大于0时,则∠OCQ逐渐变大,故∠OCA<∠OCQ.
-
科目: 来源: 题型:
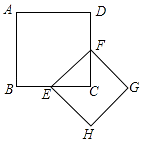
查看答案和解析>>【题目】如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
A.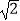 +1
+1
B.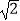
C.2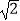 +1
+1
D.2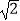
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )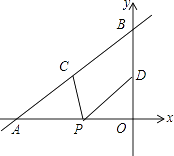
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多
 元,用
元,用 元购得的排球数量与用
元购得的排球数量与用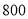 元购得的足球数量相等.
元购得的足球数量相等.⑴排球和足球的单价各是多少元?
⑵若恰好用去
 元,有哪几种购买方案?
元,有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个容量为16GB的便携式U盘的内存全部用来储数码照片,若每张照片文件大小为211KB,则这个U盘可以存储这样的数码照片张.(16GB=224KB,用2为底的幂表示结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+(3a5b3)÷(a2b)2 , 其中ab=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月29日至10月7日,2019年北京世界园艺博览会在北京延庆举行,园区内率先开展了5G网络的商用试验.已知现在4G网络在理想状态下峰值速率约是100Mbps,而5G网络峰值速率是4G网络的204.8倍,请用科学记数法表示5G网络峰值速率约为______Mbps.
相关试题

