【题目】如图,直线y= ![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )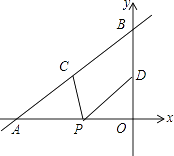
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
参考答案:
【答案】C
【解析】解:(方法一)作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
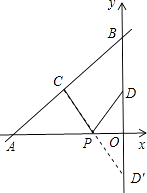
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣3,2),D′(0,﹣2),
∴有 ![]() ,解得:
,解得: 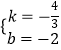 ,
,
∴直线CD′的解析式为y=﹣ ![]() x﹣2.
x﹣2.
令y=﹣ ![]() x﹣2中y=0,则0=﹣
x﹣2中y=0,则0=﹣ ![]() x﹣2,解得:x=﹣
x﹣2,解得:x=﹣ ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.
(方法二)连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
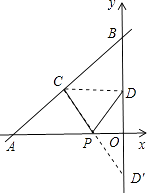
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.
(方法一)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
(方法二)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,根据三角形中位线定理即可得出点P为线段CD′的中点,由此即可得出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,垂足为C,AC=4,BC=3
 ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB. 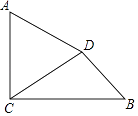
(1)线段DC=;
(2)求线段DB的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A.有三个角为直角的四边形是矩形B.矩形是中心对称图形
C.对角线相等的四边形是矩形D.矩形的对角线相等且互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
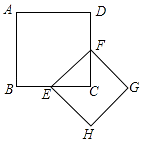
A.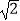 +1
+1
B.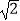
C.2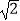 +1
+1
D.2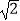
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多
 元,用
元,用 元购得的排球数量与用
元购得的排球数量与用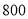 元购得的足球数量相等.
元购得的足球数量相等.⑴排球和足球的单价各是多少元?
⑵若恰好用去
 元,有哪几种购买方案?
元,有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】 抛物线
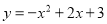 与
与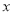 轴交于点
轴交于点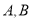 (
( 在
在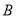 的左侧),与
的左侧),与 轴交于点
轴交于点 .
.⑴求直线
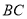 的解析式;
的解析式;⑵抛物线的对称轴上存在点
 ,使
,使 ,利用图
,利用图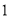 求点
求点 的坐标;
的坐标;⑶点
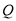 在
在 轴右侧的抛物线上,利用图
轴右侧的抛物线上,利用图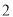 比较
比较 与
与 的大小,并说明理由.
的大小,并说明理由.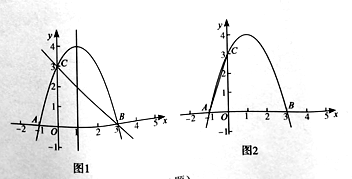
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个容量为16GB的便携式U盘的内存全部用来储数码照片,若每张照片文件大小为211KB,则这个U盘可以存储这样的数码照片张.(16GB=224KB,用2为底的幂表示结果)
相关试题

