【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s). 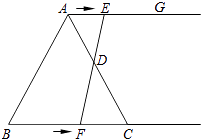
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.
参考答案:
【答案】
(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
∵在△ADE和△CDF中,
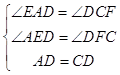 ,
,
∴△ADE≌△CDF(AAS)
(2)6;1.5
【解析】(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6, 则此时的时间t=6÷1=6(s);②四边形AFCE为直角梯形时,
(i)若CE⊥AG,则AE=3,BF=3×2=6,即点F与点C重合,不是直角梯形.
(ii)若AF⊥BC,
∵△ABC为等边三角形,
∴F为BC中点,即BF=3,
∴此时的时间为3÷2=1.5(s);
所以答案是:6;1.5.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年春学期小红同学四次中考数学测试成绩分别是:103,103,105,105,关于这组数据下列说法错误的是( )
A.平均数是104
B.众数是103
C.中位数是104
D.方差是1 -
科目: 来源: 题型:
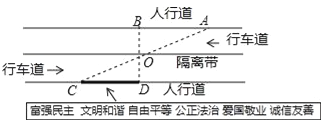
查看答案和解析>>【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A、C、B不在同一条直线上,AD∥BE
(1)如图①,当∠A=58°,∠B=118°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每一个外角都是40°,则这个多边形是( )
A. 六边形 B. 八边形 C. 九边形 D. 十边形
-
科目: 来源: 题型:
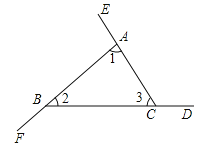
查看答案和解析>>【题目】用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2的小正方形和边长为x的大正方形放在一起.

(1)用x表示阴影部分的面积;
(2)计算当x=5时,阴影部分的面积.
相关试题

