【题目】已知,在以O为原点的直角坐标系中,抛物线的顶点为A (﹣1,﹣4),且经过点B(﹣2,﹣3),与x轴分别交于C、D两点.
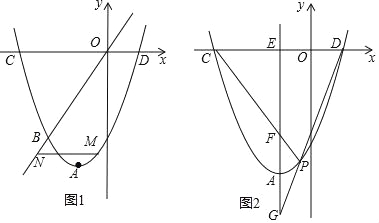
(1)求直线OB以及该抛物线相应的函数表达式;
(2)如图1,点M是抛物线上的一个动点,且在直线OB的下方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;
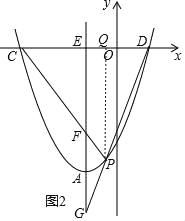
(3)如图2,过点A的直线交x轴于点E,且AE∥y轴,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G两点.当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
参考答案:
【答案】(1)直线OB解析式为y=![]() x,抛物线为y=x2+2x﹣3;(2)
x,抛物线为y=x2+2x﹣3;(2)![]() ;(3)点P运动时,EF+EG为定值8.
;(3)点P运动时,EF+EG为定值8.
【解析】
试题分析:(1)由B点坐标利用待定系数法可求直线OB解析式,利用顶点式可求得抛物线解析式;
(2)设M(t,t2+2t﹣3),MN=s,则可表示出N点坐标,由MN的纵坐标相等可得到关于s和t的关系式,再利用二次函数的性质可求得其最大值;
(3)设P(t,t2+2t﹣3),则可表示出PQ、CQ、DQ,再利用相似三角形的性质可用t分别表示出EF和EG的长,则可求得其定值.
试题解析:(1)设直线OB解析式为y=kx,由题意可得﹣3=﹣2k,解得k=![]() ,
,
∴直线OB解析式为y=![]() x,
x,
∵抛物线顶点坐标为(﹣1,﹣4),
∴可设抛物线解析式为y=a(x+1)2﹣4,
∵抛物线经过B(﹣2,﹣3),
∴﹣3=a﹣4,解得a=1,
∴抛物线为y=x2+2x﹣3;
(2)设M(t,t2+2t﹣3),MN=s,则N的横坐标为t﹣s,纵坐标为![]() ,
,
∵MN∥x轴,
∴t2+2t﹣3=![]() ,得s=
,得s=![]() =
=![]() ,
,
∴当t=![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() ;
;
(3)EF+EG=8.理由如下:
如图2,过点P作PQ∥y轴交x轴于Q,
在y=x2+2x﹣3中,令y=0可得0=x2+2x﹣3,解得x=﹣3或x=1,
∴C(﹣3,0),D(1,0),
设P(t,t2+2t﹣3),则PQ=﹣t2﹣2t+3,CQ=t+3,DQ=1﹣t,
∵PQ∥EF,
∴△CEF∽△CQP,
∴![]() ,
,
∴EF=![]() PQ=
PQ=![]() (﹣t2﹣2t+3),
(﹣t2﹣2t+3),
同理△EGD∽△QPD得![]() ,
,
∴EG=![]() PQ=
PQ=![]() ,
,
∴EF+EG=![]() (﹣t2﹣2t+3)+
(﹣t2﹣2t+3)+![]() =2(﹣t2﹣2t+3)(
=2(﹣t2﹣2t+3)(![]() )=2(﹣t2﹣2t+3)(
)=2(﹣t2﹣2t+3)(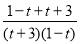 )=2(﹣t2﹣2t+3)(
)=2(﹣t2﹣2t+3)(![]() )=8,
)=8,
∴当点P运动时,EF+EG为定值8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
1号
2号
3号
4号
5号
总数
甲班
100
98
102
97
103
500
乙班
99
100
95
109
97
500
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为 ;
(2)甲班比赛成绩的方差S甲2=
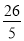 ,求乙班比赛成绩的方差;
,求乙班比赛成绩的方差;(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去兴化李中水上森林游玩.
(1)小明和小刚都在本周日上午去游玩的概率为 ;
(2)求他们三人在同一个半天去游玩的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知水星的半径约为2440000米,用科学记数法表示为( )米.
A. 0.244×107 B. 2.44×107 C. 24.4×105 D. 2.44×106
-
科目: 来源: 题型:
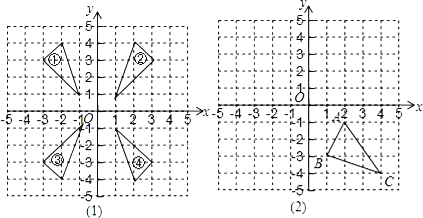
查看答案和解析>>【题目】在图(1)中编号①②③④的四个三角形中,关于y轴对称的两个三角形的编号为______;关于x轴对称的两个三角形的编号为______.在图(2)中,画出△ABC关于x轴对称的图形△A1B1C1,并分别写出点A1,B1,C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2a+3b)2=(2a-3b)2+( ),括号内的式子是( )
A.6ab
B.24ab
C.12ab
D.18ab -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,结果相等的数是( )
A.﹣12与(﹣1)2
B.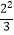 与(
与(  )2
)2
C.﹣|﹣2|与﹣(﹣2)
D.(﹣3)3与﹣33
相关试题

