搜索
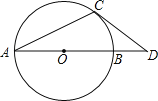
【题目】如图，AB是⊙O的直径，OA=1，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若BD=
﹣1，则∠ACD= °．
参考答案：
【答案】112.5．
【解析】
试题分析：如图，连结OC．根据切线的性质得到OC⊥DC，根据线段的和得到OD=
，根据勾股定理得到CD=1，根据等腰直角三角形的性质得到∠DOC=45°，根据等腰三角形的性质和三角形外角的性质得到∠OCA=
∠DOC=22.5°，再根据角的和得到∠ACD的度数．
解：如图，连结OC．
∵DC是⊙O的切线，
∴OC⊥DC，
∵BD=
﹣1，OA=OB=OC=1，
∴OD=，
∴CD=
=
=1，
∴OC=CD，
∴∠DOC=45°，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠OCA=∠DOC=22.5°，
∴∠ACD=∠OCA+∠OCD=22.5°+90°=112.5°．
故答案为：112.5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】圆的一条弦恰好为半径长，这条弦所对的圆周角为 度。
-
科目： 来源： 题型：
查看答案和解析>>【题目】舟山市2010﹣2014年社会消费品零售总额及增速统计图如图：
请根据图中信息，解答下列问题：
（1）求舟山市2010﹣2014年社会消费品零售总额增速这组数据的中位数．
（2）求舟山市2010﹣2014年社会消费品零售总额这组数据的平均数．
（3）用适当的方法预测舟山市2015年社会消费品零售总额（只要求列式说明，不必计算出结果）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
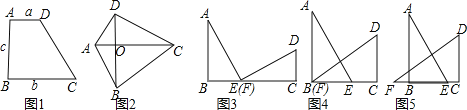
方法准备：
我们都知道：如图1，在四边形ABCD中，AD∥BC，∠B=90°，若AD=a，BC=b，AB=c，那么四边形ABCD的面积S=
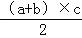．如图2，在四边形ABCD中，两条对角线AC⊥BD，垂足为O，则四边形ABCD的面积=
AC×OD+AC×OB=AC×（OD+OB）=AC×BD．解决问题：
（1）我们以a、b 为直角边，c为斜边作两个全等的直角△ABE与△FCD，再拼成如图3所示的图形，使B，E，F，C四点在一条直线上（此时E，F重合），可知△ABE≌△FCD，AE⊥DF． 请你证明：a2+b2=c2．
（2）固定△FCD，再将△ABE沿着BC平移到如图4所示的位置（此时B，F重合），请你继续证明：a2+b2=c2．
（3）当△ABE平移到如图5的位置，结论a2+b2=c2还成立吗？如果成立，请写出证明过程；如果不成立，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数学实验课上，李静同学剪了两张直角三角形纸片，进行如下的操作：
操作一：如图1，将Rt△ABC纸片沿某条直线折叠，使斜边两个端点A与B重合，折痕为DE．
（1）如果AC＝5cm，BC＝7cm，可得△ACD的周长为 ；
（2）如果∠CAD：∠BAD=1：2，可得∠B的度数为 ；
操作二：如图2，李静拿出另一张Rt△ABC纸片，将直角边AC沿直线CD折叠，使点A与点E重合，若AB＝10cm，BC＝8cm，请求出BE的长．
-
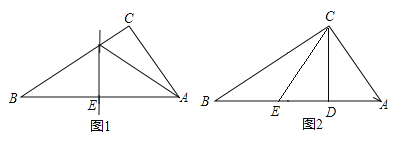
科目： 来源： 题型：
查看答案和解析>>【题目】全班同学去春游，准备租船游玩，如果比计划减少一条船，则每条船正好坐9个同学，如果比计划增加一条船，每条船正好坐6个同学，则这个班有_____个同学，计划租用_____条船。
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的方程：3x+m=2的解也是方程：x- (1-x) =1的解，求m的值.
相关试题
