【题目】如图,点A,B是数轴上的两个点,点A表示的数为﹣2,点B在点A右侧,距离A点12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)填空:①数轴上点B表示的数为 ;
②数轴上点P表示的数为 (用含t的代数式表示).
(2)设AP和PB的中点分别为点M,N,在点P的运动过程中,线段M N的长度是否发生变化?若变化,请说明理由;若不变,求出线段M N的长.
参考答案:
【答案】(1)①数轴上点B表示的数为10;②数轴上点P表示的数为 (2t﹣2);(2)线段MN的长度不发生变化,值为6.
【解析】
(1)①利用两点之间的距离计算方法求得点B所表示的数即可;
②利用左减右加的规律求得点P的所表示的数即可;
(2)分类讨论:①当点P在点A、B两点之间运动时,②当点P运动到点B的右侧时,③点P运动到点B时,利用中点的定义和线段的和差易求出MN.
解:(1)①∵10-(-2)=12,
∴数轴上点B表示的数为10;
②数轴上点P表示的数为(2t﹣2);
(2)线段MN的长度不发生变化.
①如图,当点P在点A、B之间运动时,
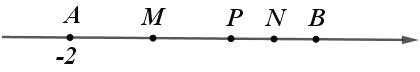
MN = MP + NP =![]() AP + PB =
AP + PB =![]() AB =
AB =![]() ×12 = 6;
×12 = 6;
②当点P运动到点B的右侧时,
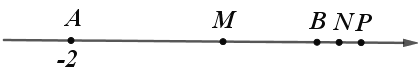
MN = MP﹣PB = ![]() AP﹣
AP﹣![]() BP =
BP = ![]() (AP﹣PB)
(AP﹣PB)
= ![]() AB =
AB = ![]() ×12 = 6;
×12 = 6;
③当点P运动到点B时,MN = MB = ![]() AB =
AB = ![]() ×12 = 6;
×12 = 6;
综上所述,线段MN的长度不发生变化,值为6.
-
科目: 来源: 题型:
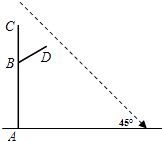
查看答案和解析>>【题目】如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短
 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程
如图,OA、BC分别是普通列车和动车从盐城开往北京的路程 与时间
与时间 的函数图象
的函数图象 请根据图中的信息,解答下列问题:
请根据图中的信息,解答下列问题: 根据图象信息,普通列车比动车早出发______h,动车的平均速度是______
根据图象信息,普通列车比动车早出发______h,动车的平均速度是______ ;
; 分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
分别求出OA、BC的函数表达式,并写出自变量x的取值范围; 动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为20 (元/个)的计算器,其销售量y (万个)与销售价格x (元/个)之间为一次函数关系,其变化如下表:
价格x (元/个)
…
30
50
…
销售量y (万个)
…
5
3
…
同时,销售过程中的其他开支(不含进价)总计40万元.若该公司要获得40万元的净利润,且尽可能让顾客得到实惠,那么销售价格应定为多少?
(注:净利润=总销售额﹣总进价﹣其他开支) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).

(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组):
(1)
 ;
;(2)
 =x﹣2;
=x﹣2;(3)
 ;
;(4)
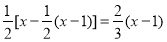 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=
 .
.
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
相关试题

