【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
参考答案:
【答案】
(1)解:∵AE=BF=x,
∴EF=AB﹣AE﹣BF=60﹣2x.
∴在Rt△GEF中,GF= ![]() EF=
EF= ![]() ×(60﹣2x)=30
×(60﹣2x)=30 ![]() ﹣
﹣ ![]() x;
x;
(2)解:∵NG= ![]() AE=
AE= ![]() x,即GH=NG=
x,即GH=NG= ![]() x,
x,
∴S= ![]() x (30
x (30 ![]() ﹣
﹣ ![]() x)=﹣2x2+60x
x)=﹣2x2+60x
=﹣2(x﹣15)2+450;
∵﹣2<0,
∴当x=15时,S最大=450;
(3)解:能放下.
理由是:当圆柱形工艺品与GHMN相切时,x=15 ![]() ,
,
此时,30 ![]() ﹣
﹣ ![]() x=30
x=30 ![]() ﹣15
﹣15 ![]() ×
× ![]() =30
=30 ![]() ﹣30>10,故一定能放下.
﹣30>10,故一定能放下.
根据题意得: ![]()
解得:15 ![]() ≤x≤30﹣5
≤x≤30﹣5 ![]() .
.
【解析】(1)主要考查切去的图形为等腰直角三角形,等腰直角三角形的边比为1:1:![]() ,根据边比的关系,即可分别写出对应边的量。
,根据边比的关系,即可分别写出对应边的量。
(2)因为剪去的为等腰直角三角形,所以对应的△FBP也为等腰直角三角形,即GH=NG,底面为正方形,即可表达出S的表达式,利用二次函数进行求最值。(3)根据圆柱工艺品的高和底面半径列出相应的不等式进行求解即可。
【考点精析】本题主要考查了二次函数的最值和正多边形和圆的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短
 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程
如图,OA、BC分别是普通列车和动车从盐城开往北京的路程 与时间
与时间 的函数图象
的函数图象 请根据图中的信息,解答下列问题:
请根据图中的信息,解答下列问题: 根据图象信息,普通列车比动车早出发______h,动车的平均速度是______
根据图象信息,普通列车比动车早出发______h,动车的平均速度是______ ;
; 分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
分别求出OA、BC的函数表达式,并写出自变量x的取值范围; 动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为20 (元/个)的计算器,其销售量y (万个)与销售价格x (元/个)之间为一次函数关系,其变化如下表:
价格x (元/个)
…
30
50
…
销售量y (万个)
…
5
3
…
同时,销售过程中的其他开支(不含进价)总计40万元.若该公司要获得40万元的净利润,且尽可能让顾客得到实惠,那么销售价格应定为多少?
(注:净利润=总销售额﹣总进价﹣其他开支) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B是数轴上的两个点,点A表示的数为﹣2,点B在点A右侧,距离A点12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)填空:①数轴上点B表示的数为 ;
②数轴上点P表示的数为 (用含t的代数式表示).
(2)设AP和PB的中点分别为点M,N,在点P的运动过程中,线段M N的长度是否发生变化?若变化,请说明理由;若不变,求出线段M N的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组):
(1)
 ;
;(2)
 =x﹣2;
=x﹣2;(3)
 ;
;(4)
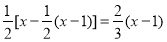 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB=
 .
.
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).

(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为 ,求点D的坐标;
,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
相关试题

