搜索
【题目】如图，已知AD是等腰△ABC底边BC上的高，sinB= 
，点E在AC上，且AE：EC=2：3，则tan∠ADE=（ ） 
A.
B.
C.
D.
参考答案：
【答案】B
【解析】解：如图．作EF∥CD交AD于F点．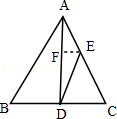 
∵sinB=sinC= 
= 
，
∴设AD=4x，则AC=5x，CD=3x，
∵ 
= 
= 
，
∴FD= 
x，AF= 
x．
∵ 
= 
= 
，
∴EF= 
x．
∴tan∠ADE= 
= 
，
故选：B．
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如图的折线统计图，则符合这一结果的实验最有可能的是（ ）
A.在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子，向上的面点数是4
-
科目： 来源： 题型：
查看答案和解析>>【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两行环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元，
（1）求购买A型和B型公交车每辆各需多少万元？
（2）预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1220万元，且确保这10辆公交车在该线路的年均载客量总和不少于650万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊙O中，AB是⊙O的直径，AB＝10，
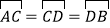，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE＝60°；②∠CED＝
∠DOB；③DM⊥CE；④CM＋DM的最小值是10，上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
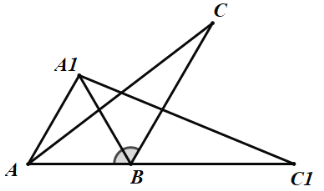
查看答案和解析>>【题目】如图，将一个钝角△ABC（其中∠ABC＝120°）绕
点B顺时针旋转得△A1BC1，使得C点落在AB的延长线上的点C1处，连结AA1．
（1）写出旋转角的度数；
（2）求证：∠A1AC＝∠C1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有形状、大小和质地都相同的四张卡片
，
，
，
，正面上分别写有四个实数
，
，
，
将这四张卡片背面向上洗匀，从中随机抽取一张（不放回），接着再随机抽取一张．（1）画树形图或列表法表示抽取两张卡片可能出现的所有情况（卡片可用
、、、表示）；（2）求取到的两个数都是无理数的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC外切于⊙O，切点分别为点D，E，F，∠A＝60°，BC＝7，⊙O的半径为
.求：（1）求BF+CE的值； （2）求△ABC的周长．
相关试题
