【题目】如图,等边三角形 ABC 的边长为 3,过点 B 的直线 l⊥AB,且△ABC 与△A′BC′关于直线 l 对称,D 为线段 BC′上一动点,则 AD+CD 的最小值是_____.

参考答案:
【答案】6
【解析】
作点A关于直线BC′的对称点A1,连接A1C交直线BC与点D,由图象可知点D在C′B的延长线上,由此可得出当点D与点B重合时,AD+CD的值最小,由此即可得出结论,再根据等边三角形的性质算出AB+CB的长度即可.
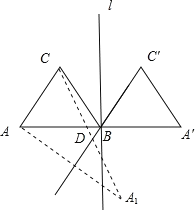
作点A关于直线BC′的对称点A1,连接A1C交直线BC与点D,如图所示.
由图象可知当点D在C′B的延长线上时,AD+CD最小,
而点D为线段BC′上一动点,
∴当点D与点B重合时AD+CD值最小,
此时AD+CD=AB+CB=3+3=6.
故答案为:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:

(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60 m到达河边B处取水,然后沿另一方向走80 m到达菜地C处浇水,最后沿第三方向走100 m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.

-
科目: 来源: 题型:
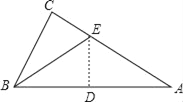
查看答案和解析>>【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
A. 2
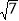 B.
B. 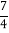 C.
C.  D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ABE绕点
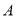 顺时针旋转90
顺时针旋转90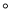 后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△
后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△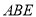 ≌△
≌△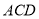 ③AD平分∠EDF ④
③AD平分∠EDF ④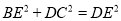 ;正确的有______________(填序号)
;正确的有______________(填序号)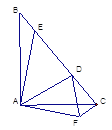
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O直径,D是
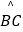 的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.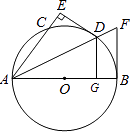
(1)求证:直线DE与⊙O相切;
(2)已知DG⊥AB且DE=4,⊙O的半径为5,求tan∠F的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
相关试题

