搜索
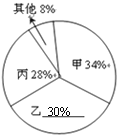
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
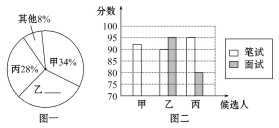
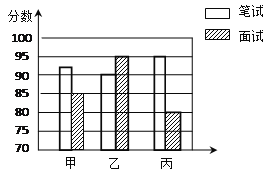
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完整的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二.
(2)请计算每名候选人的得票数.
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2∶5∶3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
参考答案：
【答案】（1）如下图；（2）（2）甲68票，乙60票数，丙56票；（3）乙
【解析】
试题（1）根据扇形统计图及统计表中的数据特征求解即可；
（2）用200乘以扇形统计图中对应的百分比即可求得结果；
（3）先根据加权平均数的计算公式求得三名候选人的平均成绩，再比较即可作出判断.
解：（1）
（2）甲的票数是：
（票）
乙的票数是：
（票）
丙的票数是：
（票）；
（3）甲的平均成绩
乙的平均成绩
丙的平均成绩
∵乙的平均成绩最高
∴应该录取乙.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，分别以点A和点B为圆心，以大于
AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，若△ADC的周长为10，AB=6，则△ABC的周长为（ ） 
A.6
B.12
C.16
D.20 -
科目： 来源： 题型：
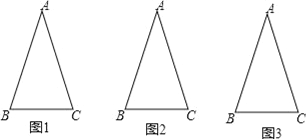
查看答案和解析>>【题目】如图，△ABC中，AB=AC，∠A=36°，称满足此条件的三角形为黄金等腰三角形．请完成以下操作：（画图不要求使用圆规，以下问题所指的等腰三角形个数均不包括△ABC）
（1）在图1中画1条线段，使图中有2个等腰三角形，并直接写出这2个等腰三角形的顶角度数分别是 度和 度；
（2）在图2中画2条线段，使图中有4个等腰三角形；
（3）继续按以上操作发现：在△ABC中画n条线段，则图中有 个等腰三角形，其中有 个黄金等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明家1至6月份的用水量统计如图所示，关于这组数据，下列说法错误的是（ ）．
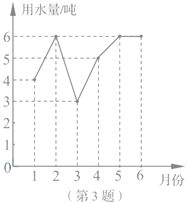
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是
-
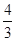
科目： 来源： 题型：
查看答案和解析>>【题目】如图是地铁昌平线路图．在图中，以正东为正方向建立数轴，有如下四个结论：
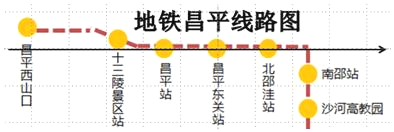
①当表示昌平东关站的点对应的数为0，表示昌平站的点对应的数为﹣1.5时，表示北邵洼站的点对应的数为1.2；
②当表示昌平东关站的点对应的数为0，表示昌平站的点对应的数为﹣15时，表示北邵洼站的点对应的数为12；
③当表示昌平东关站的点对应的数为1，表示昌平站的点对应的数为﹣14时，表示北邵洼站的点对应的数为13；
④当表示昌平东关站的点对应的数为2，表示昌平站的点对应的数为﹣28时，表示北邵洼站的点对应的数为26．
上述结论中，所有正确结论的序号是（ ）
A. ①②③B. ②③④C. ①④D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为（ ）
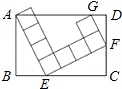
A.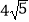
B.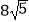
C.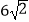
D.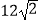
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次
组别
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
(1)请根据上表中的数据完成下表.(注:方差的计算结果精确到0.1)
平均数
中位数
方差
甲组
乙组
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图.
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况进行简要评价.
相关试题
