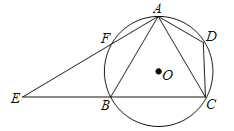
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证△ADC∽△EBA,只要证明两个角对应相等就可以.可以转化为证明且![]() 就可以;
就可以;
(2)A是![]() 的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
的中点,的中点,则AC=AB=8,根据△CAD∽△ABE得到∠CAD=∠AEC,求得AE,根据正切三角函数的定义就可以求出结论.
试题解析:(1)证明:∵四边形ABCD内接于⊙O,∴∠CDA=∠ABE.
∵![]() ,∴∠DCA=∠BAE,∴△ADC∽△EBA;
,∴∠DCA=∠BAE,∴△ADC∽△EBA;
(2)解:∵A是![]() 的中点,∴
的中点,∴![]() ,∴AB=AC=8,∵△ADC∽△EBA,∴∠CAD=∠AEC,
,∴AB=AC=8,∵△ADC∽△EBA,∴∠CAD=∠AEC,![]() ,即
,即![]() ,∴AE=
,∴AE=![]() ,∴tan∠CAD=tan∠AEC=
,∴tan∠CAD=tan∠AEC=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是 .
-
科目: 来源: 题型:
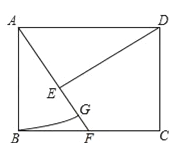
查看答案和解析>>【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=
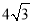 ,求DE的长.
,求DE的长. 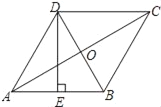
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为a,b,c,记
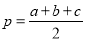 ,那么三角形的面积为
,那么三角形的面积为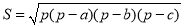 . ①
. ①古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式:
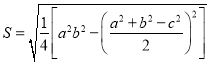 . ②
. ②下面我们对公式②进行变形:
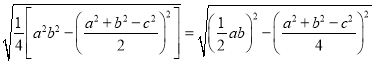
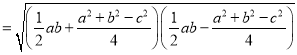
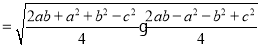
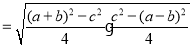
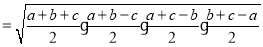
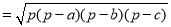 .
.这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
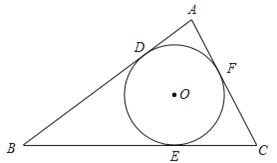
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件:①射击1次,中靶;②打开电视,正在播广告;③地球上,太阳东升西落.其中必然事件的有_____.(只填序号).
相关试题

