
【题目】某种水果进价为每千克15元,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克.设销售单价为![]() (元),每天的销售量为
(元),每天的销售量为![]() (千克),每天获利为
(千克),每天获利为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
之间的函数关系式;该水果定价为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种水果每天的销售量不低于40千克,求商家每天销售利润的最大值是多少元?
【答案】(1)![]() ;(2)该水果售价定为每千克23元时,每天的销售利润最大,最大利润是245元;(3)商家每天销售利润的最大值是240元.
;(2)该水果售价定为每千克23元时,每天的销售利润最大,最大利润是245元;(3)商家每天销售利润的最大值是240元.
【解析】
(1)根据“销售单价每上涨1元,日销售量就减少5千克”即可列出y与x之间的函数关系式;
(2)根据“利润=每千克的利润×销售数量”即可列出w与x之间的函数关系式,将二次函数解析式转化成顶点式即可得出答案;
(3)先根据销售量求出自变量x的取值范围,再根据二次函数的增减性进行解答即可.
解:(1)根据题意得:![]() ;
;
(2)根据题意得:![]() ,
,
![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为:
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为245;
有最大值,最大值为245;
(3)由题意得:![]() ,
,
解得![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值,其最大值为
有最大值,其最大值为![]() (元).
(元).
答:商家每天销售利润的最大值是240元.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
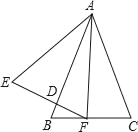
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠C;②DF=BF;③△ADE∽△FDB;④∠BFD=∠CAF.其中正确的结论是_____(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
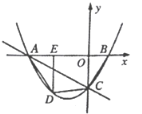
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,点
,点![]() 是抛物线上一点,过点
是抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在第三象限,设
在第三象限,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,若
,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
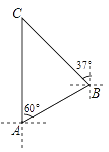
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com