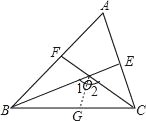
【题目】△ABC中,∠A=60°,平分线BE、CF相交于O,求证:OE=OF.

参考答案:
【答案】见解析
【解析】
由∠A=60°,BE、CF是角平分线就可以得出∠BOC=120,进而得出∠BOF=∠COE=60°,在BC上取点G,使BG=BF,就可以得出△BOF≌△BOG,就可以得出OF=OG,∠BOF=∠1=60°,进而求出∠2=60°,得出∠2=∠COE,得出△COE≌△COG,就有OE=OG,进而得出结论.
在BC上取点G,使BG=BF,
∵BE平分∠ABC,CF∠ACB,
∴∠ABE=∠CBE=![]() ∠ABC,∠ACF=∠BCF=
∠ABC,∠ACF=∠BCF=![]() ∠ACB,
∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴![]() ∠ABC+
∠ABC+![]() ∠ACB=60°,
∠ACB=60°,
∴∠BOC=120°,
∴∠BOF=∠COE=60°,
在△BOF和△BOG中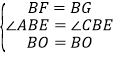 ,
,
∴△BOF≌△BOG(SAS),
∴OF=OG,∠BOF=∠1,
∴∠1=60°,
∴∠2=60°,
∴∠2=∠COE,
在△COE和△COG中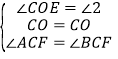 ,
,
∴△COE≌△COG(ASA),
∴OE=OG.
∴OE=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,AD=AE,BE、CE相交于点F,则图中全等三角形共有( )对.

A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图
 所示放置,图
所示放置,图 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC, 请找出图
请找出图 中的全等三角形,并给予说明
中的全等三角形,并给予说明 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母 ;
; 试说明:
试说明: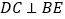 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能够使△BPE与△CQP全等;此时点Q的运动速度为多少.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①∠1=∠2;②BE=CF;③△CAN≌△ABM;④CD=DN其中正确的结论是( )

A. ①② B. ②③ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.

(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
相关试题

